Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento Angular

Ver Teoria
Exercício 101234567891112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Momento Angular

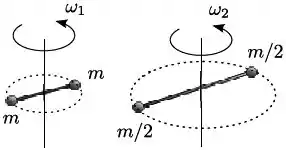
Um haltere é formado por duas partículas de massa m , ligadas por uma barra rígida de massa desprezível e comprimento 2 a , e gira com velocidade angular ω 1 em torno de um eixo fixo perpendicular a barra e passando pelo seu ponto médio. Um segundo haltere é formado por duas partículas de massa m / 2 , ligadas por uma barra rígida de massa desprezível e comprimento 4 a , e gira com velocidade angular ω 2 em torno de um eixo fixo perpendicular a barra e passando pelo seu ponto médio. Considerando que os halteres têm o mesmo momento angular, podemos afirmar que:

  1. ω 2 = ω 1
  2. ω 2 = 2 ω 1
  3. ω 2 = ω 1 / 2
  4. ω 2 = 2 ω 1
  5. ω 2 = ω 1 / 2

Passo 1

Vamos calcular momento angular do haltere 1 e do haltere 2 . Começando pelo primeiro, devemos inicialmente achar seu momento de inércia

I 1 = m a 2 + m a 2

Isso porque a massa da barra é desprezível

I 1 = 2 m a 2

Seu momento angular fica

L 1 = I 1 ⋅ ω 1

L 1 = 2 m a 2 ω 1

Passo 2

Agora vamos para o segundo halter, devemos inicialmente achar seu momento de inércia

I 2 = m 2 2 a 2 + m 2 2 a 2

Isso porque a massa da barra é desprezível

I 2 = 4 m a 2 2 + 4 m a 2 2

I 2 = 4 m a 2

Seu momento angular fica

L 2 = I 2 ⋅ ω 2

L 2 = 4 m a 2 ω 2

Passo 3

Como os momentos angulares são iguais

L 1 = L 2

2 m a 2 ω 1 = 4 m a 2 ω 2

ω 1 = 2 ω 2

ω 2 = ω 1 2

Resposta

Letra C

Exercícios de Livros Relacionados

Um bloco homogênea de granito em forma de livro possui faces de 20c m por 15c m e uma espessura de 1,2c m . A massa específica (massa por unidade de volume) do granito é 2,64g / c m 3 . O bloco gira e
10.19E Calcule o momento angular orbital da Terra em termos da constante de Planck.
Um ponto na borda de um rebolo com 0,75m de diâmetro muda de velocidade, a uma taxa constante, de 12m / s para 25m / s em 6,2s . Qual é a aceleração angular média do rebolo?
Em um certo instante, uma partícula de 0,80k g está situada na posição r → = 2,0m i ^ + 3,0m j ^ . O momento linear da partícula está no plano x y e tem um módulo de 2,4k g ∙ m / s e uma direção de 11
Em um certo instante, a força F → = 4 j → N age sobre um objeto de 0,25 k g cujo vetor posição é r → = 2 i → - 2 k → e cujo vetor velocidade é v → = - 5 i → + 5 k → . Em relação à origem e em termos d