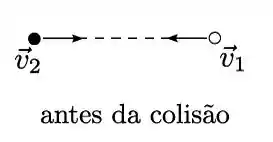
Dois objetos de mesma massa e dimensões desprezíveis colidem no espaço sideral, na ausência de forças externas. A figura mostra um sistema de eixos de um referencial inercial, com seus unitários e . Antes da colisão os objetos se movem ao longo do eixo com velocidades de sentidos opostos, como indicados na figura, e módulos e , nos quais é uma constante dada. Após a colisão, um os objetos adquire velocidade (na figura de baixo apenas um dos objetos é mostrado).
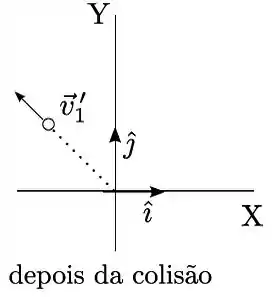
- Determine a velocidade do outro objeto após a colisão, expressando sua resposta em termos da constante e dos unitários e .
- Determine a razão entre a energia cinética do par de objetos depois da colisão e sua energia cinética antes da colisão; esta colisão é elástica ou inelástica?
Passo 1
a)
Como não temos ação de forças externas o momento linear se conserva. Vamos calcular antes da colisão
Onde
E
Resultando em
Passo 2
Agora vamos calcular o momento linear depois da colisão
Onde
E
Resultando em
Passo 3
Como os momentos lineares se conservam
Passo 4
b)
Vamos ter nas energias cinéticas as seguintes contas, começando pela energia cinética antes da colisão
Passo 5
Agora para a energia cinética após a colisão
Repara que vamos usar o módulo da velocidade na energia cinética, sabemos que
Vamos achar agora
Não precisamos fazer a raiz já que na fórmula está ao quadrado
Passo 6
Vamos ter a seguinte razão para
Como a energia cinética não é igual ele é uma colisão inelástica, no caso parcialmente inelástica.
Resposta
colisão inelástica, no caso parcialmente inelástica.