Dinâmica de Rotação
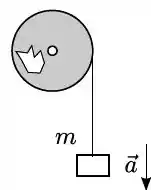
Um corpo de massa está suspenso por um fio de massa desprezível enrolado numa polia de raio . A polia consiste em um disco rígido do qual foi retirado um pedaço, como mostra a figura. A polia tem massa e gira sem atrito em torno de um eixo que passa pelo seu centro. Se a massa desce com aceleração de módulo , o momento de inércia da polia é:
- ;
- ;
- ;
- ;
- ;
Passo 1
Temos que fazer a soma das forças no bloco e a soma dos torques no disco. Começando pelo bloco.
Se o bloco está caindo, e considerando o módulo da sua aceleração como temos
Passo 2
No disco a única força que faz torque é a tração, que faz o bloco girar no sentido horário. Se o módulo da aceleração angular é teremos
Lembrando que
Vamos ter
Passo 3
Substituindo esse valor da tração na primeira equação
Resposta
Letra D
Exercícios de Livros Relacionados
Um dispositivo para medir o momento de inércia de um corpo é mostrado na figura. A plataforma circular está presa a um tambor concêntrico de raio R , plataforma e tambor estando livres para girar em t
Um cilindro de uniforme, de massa M e raio R , tem um fio enrolado no seu entorno. O fio é mantido fixo, enquanto o cilindro cai verticalmente, como mostrado na figura. (a) Mostre que a aceleração do
A extremidade superior do fio enrolado em redor do cilindro da figura está segura por uma mão que acelera para cima, de modo que o centro de massa do cilindro não se move, enquanto o cilindro gira. De
Calcule o efeito da massa M da polia, de raio R , sobre o sistema do Cap. 4, Probl. 12 (fig); a masssa m , que desliza sem atrito está ligado à massa suspensa m ' pelo fio que passa sobre a polia. Det
Um bloco de massa m , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação θ em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio R e massa M ,