Dinâmica de Rotação
Um disco homogêneo de massa e raio encontra-se sobre uma mesa horizontal completamente lisa, sem estar preso a ela. Em um dado instante duas forças estão aplicadas tangencialmente na beirada do disco, uma em um ponto diametralmente oposto ao ponto de aplicação da outra. Sabendo que o momento de inércia do disco relativo ao eixo perpendicular a ele que passa pelo seu centro de massa é , e denotado por e os módulos respectivos da aceleração do centro de massa do disco e da aceleração angular de rotação em torno do eixo no instante considerado, podemos dizer que:
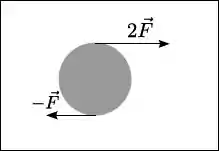
- e ;
- e ;
- e ;
- e ;
- e
Passo 1
Temos a soma das forças para encontrar a e a soma dos torques para achar
Começando pela aceleração do centro de massa
Passo 2
Vamos agora para a rotação
Isso porque as duas forças fazem o disco girar no sentido horário
O módulo da aceleração angular é , então
Lembrando que para um disco
Então
Vale a pena comentar que nesse caso o centro de rotação não é o centro de massa do disco, por isso devemos fazer as equações.
Resposta
Letra B