A figura mostra um carrinho de massa , sobre um trilho de ar, que comprime de uma mola de constante elástica . O carrinho está inicialmente preso ao suporte do trilho por um fio. O fio é cortado, e a mola expande-se empurrando o carrinho. Ao passar pela posição de equilíbrio da mola, , o carrinho perde contato com a mola. No trajeto até perder contato com a mola, o impulso fornecido ao carrinho foi igual a:
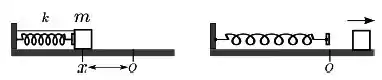
- ;
- ;
- ;
- ;
- ;
Passo 1
Para calcular o impulso vamos usar a fórmula do impulso pelo momento linear
Ou seja, é só achar as velocidades antes e depois do impulso.
Passo 2
Começando pela velocidade inicial, como o bloco parte do repouso, então
Passo 3
Podemos achar a velocidade quando o bloco descola da mola fazendo a conservação da energia mecânica, isso acontece porque não temos forças dissipativas como o atrito atuando, isso porque ele está em um trilho de ar. Sempre que ele falar de trilhos de ar lembra que não existe atrito.
Inicialmente teremos só a energia potencial da mola e depois de descolar da mola teremos só a energia cinética do carrinho.
Então
Como o sentido é para direita
Passo 4
Então o impulso será
Dando uma arrumada, vamos entrar com o na raiz:
O módulo é então
Resposta
Letra D