Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Posição do Centro de Massa

Ver Teoria
Exercício 10123456789111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970

Enunciado

Sistema de Partículas

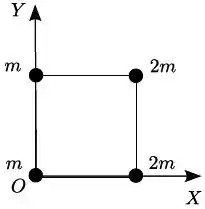
Quatro contas estão presas nos vértices de um arame quadrado de lado a , como mostra a figura. Duas contas possuem massa m e as outras duas massa 2 m . Desprezando a massa do arame e de acordo com o sistema de referência indicado na figura, a posição do centro de massa do arranjo é:

  1. x c m = 2 a / 5 e y c m = a / 2 ;
  2. x c m = a / 5 e y c m = a / 2 ;
  3. x c m = a / 4 e y c m = a / 2 ;
  4. x c m = a / 2 e y c m = a / 2 ;
  5. x c m = 2 a / 3 e y c m = a / 2 ;

Passo 1

O eixo cartesiano já foi dado pelo enunciado, então vamos nos basear nele.

Repara que o arranjo é composto por 4 contas, vamos numera-los para nos organizar.

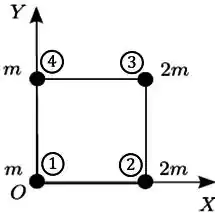
Passo 2

Vamos ter

E i x o   x x 1 = 0 x 2 = a x 3 = a x 4 = 0

E i x o   y y 1 = 0 y 2 = 0 y 3 = a y 4 = a

Passo 3

Usando a fórmula para as coordenadas do centro de massa vamos ter

x C M = x 1 ⋅ m 1 + x 2 ⋅ m 2 + x 3 ⋅ m 3 + x 4 ⋅ m 4 m 1 + m 2 + m 3 + m 4

Lembrando que

m 1 = m 4 = m

m 2 = m 3 = 2 m

Então

x C M = 0 ⋅ m + a ⋅ 2 m + a ⋅ 2 m + 0 ⋅ m m + m + 2 m + 2 m

x C M = 2 m a + 2 m a 6 m

x C M = 2 a 3

Passo 4

Agora fazendo no e i x o   y

y C M = y 1 ⋅ m 1 + y 2 ⋅ m 2 + y 3 ⋅ m 3 + y 4 ⋅ m 4 m 1 + m 2 + m 3 + m 4

Então

x C M = 0 ⋅ m + 0 ⋅ 2 m + a ⋅ 2 m + a ⋅ m m + m + 2 m + 2 m

y C M = 2 m a + m a 6 m

y C M = a 2

Resposta

Letra E

Exercícios de Livros Relacionados

A Fig. 9-35 mostra um sistema de três partículas de massas m 1 = 3,0k g , m 2 = 4,0k g e m 3 = 8,0k g . As escalas do gráfico são definidas por x s = 2,0m e y s = 2,0m . Quais são (a) a coordenada x e
Um pedaço uniforme de folha de metal é moldado conforme mostrado na Figura P8.34. Calcule as coordenadas x e y do centro de massa da folha.
Uma haste de 30,0c m de comprimento tem densidade linear (massa por comprimento) definida por λ=50,0+20,0x em que x é a distância a partir de uma extremidade, medida em metros, e λ expressa g r a m a
Duas partículas de 3,0k g têm velocidades v → 1 = 2,0 m s i ^ + 3,0 m s j ^ e v → 2 = 4,0 m s i ^ - 6,0 m s j ^ . Encontre a velocidade do centro de massa do sistema.
Quatro corpos estão situados ao longo do eixo y da seguinte forma: um de 2,00k g está a + 3,00m , um de 3,00k g está a + 2,50m , o terceiro, de 2,50k g , está na origem, e o quarto, de 4,00k g , está