PF de Física 1 da UFRJ - 2014.2

Uma nave espacial isolada tem um eixo de simetria em relação ao qual seu momento de inércia é . A nave gira em torno desse eixo com velocidade angular constante de módulo . Aciona-se um mecanismo interno da nave que reduz seu tamanho, sem perder sua simetria relativa ao eixo de rotação, de modo que ao final seu momento de inércia relativo a esse eixo se reduz a . A velocidade angular final da nave no tamanho final é dada por

(a)

(b)

(c)

(d)

(e)

Um bloco de massa é puxado por uma mola ideal em movimento retilíneo sobre uma superfície horizontal com aceleração constante de módulo . O coeficiente de atrito cinético entre o bloco e a superfície é . A elongação da mola é

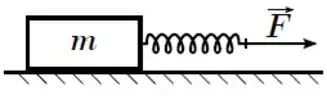
(a)

(b)

(c)

(d)

(e)

Uma partícula se move ao longo do eixo e o gráfico de sua velocidade em função do tempo em um intervalo de a é o segmento de reta indicado na figura. Podemos afirmar que nesse intervalo de tempo a aceleração da partícula e o seu deslocamento são dados por

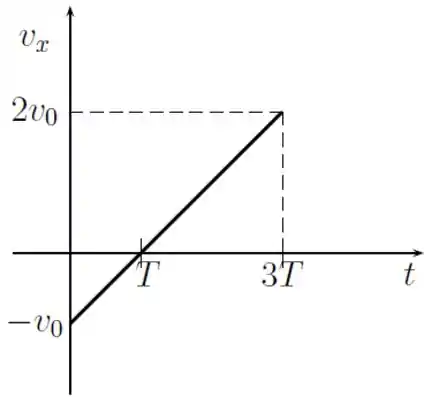
(a) e

(b) e

(c) e

(d) e

(e) e

Um cilindro rígido e homogêneo de massa e raio está sobre uma superfície horizontal e pode girar livremente em torno de seu eixo de simetria longitudinal, como indicado na figura. O eixo está preso a uma extremidade de um fio ideal que passa por uma polia ideal e tem em sua outra extremidade um bloco suspenso de massa . O bloco desce verticalmente com aceleração para baixo e o cilindro rola sem deslizar sobre a superfície horizontal devido ao seu atrito com ela. O momento de inércia do cilindro relativo ao eixo de simetria é . Considere como dados e o módulo da aceleração da gravidade.

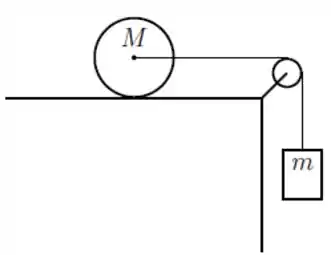
a) Indique todas as forças externas que atuam sobre o bloco e sobre o cilindro.

b) Calcule o módulo da aceleração do bloco;

c) Calcule o módulo da força de atrito sobre o cilindro e indique o seu sentido.

Três forças, , e , de mesmo módulo , agem sobre uma placa quadrada de lado , como ilustra a figura; as forças estão no plano da placa. Usando os unitários e indicados na figura, indique a opção correta para o torque total dessas forças relativo ao centro da placa.

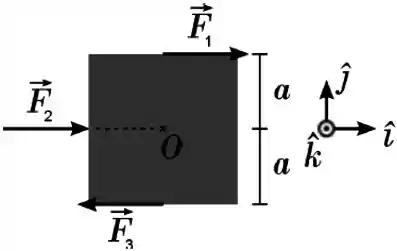
(a)

(b)

(c)

(d)

(e)

A figura mostra uma rampa com um trecho horizontal e o ponto a uma altura do trecho horizontal. Um bloco de massa é abandonado em repouso sobre a rampa no ponto e um bloco idêntico está em repouso sobre a rampa entre e .

A parte do trecho horizontal tem comprimento , e coeficiente de atrito cinético com os blocos, já o restante da rampa é totalmente liso.Ao final do trecho horizontal , entre os pontos e , encontra-se uma mola de constante elástica fixada à rampa em .O bloco abandonado em sofre uma colisão perfeitamente inelástica com o outro bloco e o conjunto se move na horizontal até atingir a mola e comprimi-la até parar.

Considere como dados e o módulo da aceleração da gravidade.

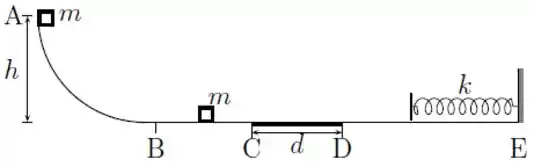
Considerando as dimensões dos blocos desprezíveis, calcule

a) a velocidade do bloco abandonado em imediatamente antes de colidir com o outro bloco;

b) a velocidade do conjunto imediatamente depois da colisão;

c) a velocidade do conjunto imediatamente antes de colidir com a mola;

d) o máximo comprimento de compressão da mola.

Um pêndulo cônico é constituído por uma partícula presa a um fio ideal que faz um ângulo com a vertical, de modo que a partícula esteja em movimento circular uniforme em um plano horizontal com o centro da trajetória no ponto da vertical, como indica a figura. Em um dado instante, em que a partícula está em um ponto , sua aceleração é um vetor de

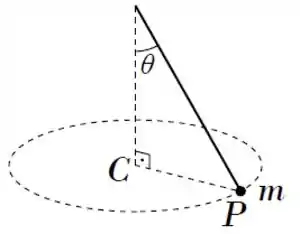
(a) módulo , vertical apontando pra baixo

(b) módulo , apontando de pra

(c) módulo , apontando de pra

(d) módulo , apontando de pra

(e) módulo , apontando de pra

Duas partículas com velocidades iniciais perpendiculares (figura) colidem de forma totalmente inelástica. Seja o momento linear total do sistema composto pelas duas partículas (, seu módulo) e a energia cinética total deste sistema. Comparando os valores de e antes e depois da colisão, pode-se afirmar que

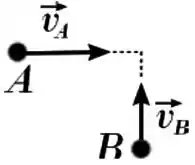
(a) é conservado, é reduzido, porém não a zero.

(b) é conservado, é conservado;

(c) é reduzido a zero, é reduzido a zero;

(d) é conservado, é reduzido a zero;

(e) é reduzido, porém não a zero, é reduzido, porém não a zero;

Sejam dois caminhos diferentes e que começam em um ponto e terminam em um ponto (na figura tem sentido indicado por seta simples e , por seta dupla). Sejam e os trabalhos não nulos realizados por uma força conservativa sobre uma partícula que percorra os caminhos e , respectivamente.

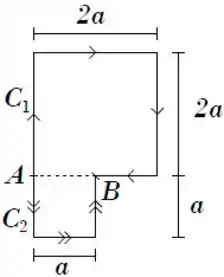
Pode-se afirmar que

(a)

(b)

(c)

(d)

(e)

Um rojão de massa explode após seu lançamento em apenas dois pedaços, um com o dobro da massa do outro. O rojão imediatamente antes da explosão tem velocidade e o pedaço de menor massa imediatamente após a explosão tem velocidade . A velocidade do pedaço de maior massa imediatamente após a explosão é

(a)

(b)

(c)

(d)

(e)

Parado numa rua, embaixo de uma marquise, um homem vê as gotas de chuva caindo verticalmente com velocidade constante de módulo . Ao atravessar a rua (nivelada horizontalmente e plana) correndo em linha reta ele percebe que as gotas de chuva, durante a travessia, caem com um ângulo em relação à horizontal. Se ele atravessou a rua com velocidade de módulo constante em relação à Terra, a resposta correta que permite obter o ângulo , é

(a)

(b)

(c)

(d)

(e)

Numa estrada horizontal o módulo da velocidade máxima com que um carro pode fazer uma certa curva circular sem derrapar é igual a . Se num dia de inverno, em razão da presença de gelo na pista, o coeficiente de atrito estático entre os pneus do carro e a estrada fica reduzido à metade, o módulo da velocidade máxima com que o carro pode fazer a mesma curva sem derrapar é igual a

(a)

(b)

(c)

(d)

(e)