Dinâmica de Rotação
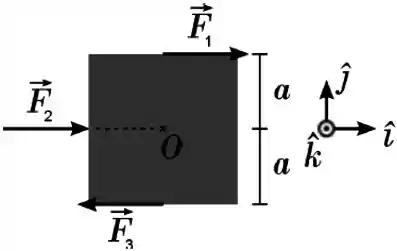
Três forças, , e , de mesmo módulo , agem sobre uma placa quadrada de lado , como ilustra a figura; as forças estão no plano da placa. Usando os unitários e indicados na figura, indique a opção correta para o torque total dessas forças relativo ao centro da placa.
(a)
(b)
(c)
(d)
(e)
Passo 1
O torque total é a soma dos torque das 3 forças:
Lembrando que o torque é dado por:
sendo o sentido positivo o anti-horário e o sentido negativo o horário, e o braço da alavanca.
Então vamos calcular esses torques! ;)
Passo 2
Começando pela força .
O ponto de aplicação dela fica a uma distância do centro , então é o braço da alavanca.
E a força gera uma rotação no sentido horário, logo o torque é negativo.
Portanto, obtemos
Passo 3
Vamos pra força .
Ih, ela está na direção do centro , então o braço da alavanca é zero!
Então o torque da é nulo:
Passo 4
Então só falta a !
Assim como pra , o braço da alavanca também é , e a rotação gerada também é no sentido horário, então o torque realizado pela é igual ao torque da :
Passo 5
Beleza, então somando tudo temos:
Resposta
Alternativa (c)