Movimento Relativo e Referencial
Parado numa rua, embaixo de uma marquise, um homem vê as gotas de chuva caindo verticalmente com velocidade constante de módulo . Ao atravessar a rua (nivelada horizontalmente e plana) correndo em linha reta ele percebe que as gotas de chuva, durante a travessia, caem com um ângulo em relação à horizontal. Se ele atravessou a rua com velocidade de módulo constante em relação à Terra, a resposta correta que permite obter o ângulo , é
(a)
(b)
(c)
(d)
(e)
Passo 1
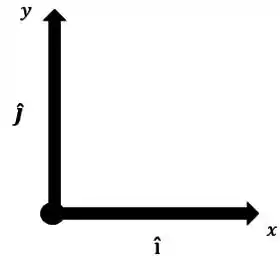
Temos um problema de velocidade relativa em 2 dimensões, então um bom reflexo é definir os eixos e os seus vetores unitários.
Vou fazer isso da forma padrão, o eixo apontando pra direita, com vetor unitário , e o eixo apontando pra cima, com vetor unitário :
Passo 2
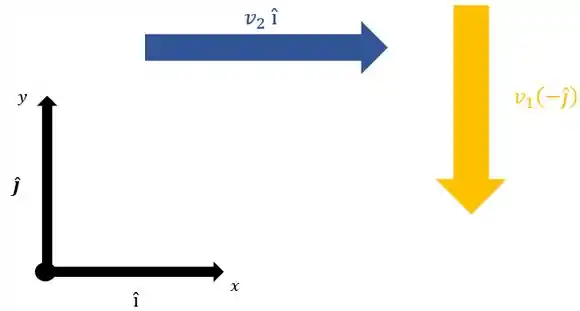
Vamos primeiro analisar as velocidades das gotas de chuva e do homem no referencial da Terra.
As gotas de chuva caem verticalmente pra baixo, com velocidade de módulo , então a velocidade delas é .
Já o homem anda na horizontal (vamos supor pra direita), com velocidade de módulo . Então sua velocidade é .
Passo 3
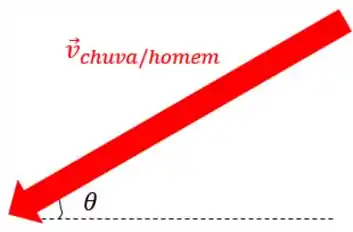
Mas no referencial do homem, as gotas de chuva agora caem com um ângulo em relação à horizontal, com uma velocidade que vamos chamar de .
Passo 4
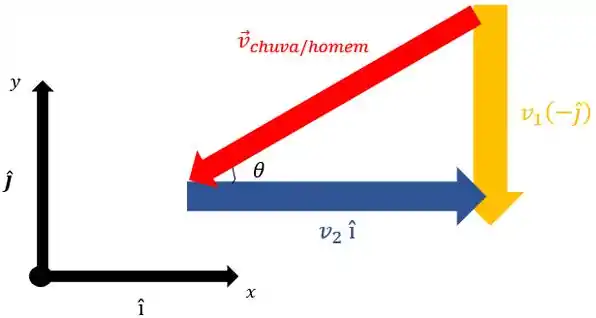
Vamos montar um diagrama vetorial com as 3 velocidades pra ver como é que ficou:
Passo 5
Então pra achar a tangente de basta aplicar uma trigonometria básica:
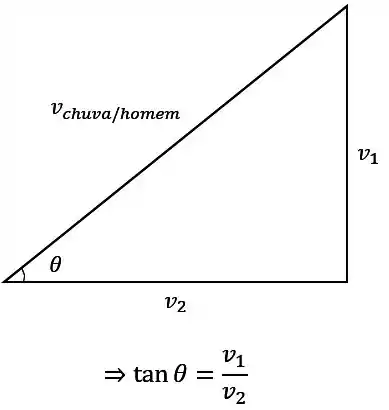
Resposta
Alternativa (e)