Duas partículas com velocidades iniciais perpendiculares (figura) colidem de forma totalmente inelástica. Seja o momento linear total do sistema composto pelas duas partículas (, seu módulo) e a energia cinética total deste sistema. Comparando os valores de e antes e depois da colisão, pode-se afirmar que
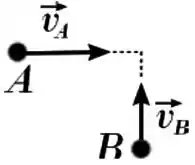
(a) é conservado, é reduzido, porém não a zero.
(b) é conservado, é conservado;
(c) é reduzido a zero, é reduzido a zero;
(d) é conservado, é reduzido a zero;
(e) é reduzido, porém não a zero, é reduzido, porém não a zero;
Passo 1
Geralmente, quando é pra considerar alguma força externa, o enunciado menciona. Mas aqui ele não falou nada, então vamos assumir que não tem nenhuma força externa atuando no sistema.
Portanto, o momento linear se conserva. Já dá pra eliminar as alternativas (c) e (e)!
Passo 2
Agora vamos dar uma olhada na energia cinética.
A alternativa (b) fala que ela é conservada, mas isso é falso! A energia cinética só é conservada numa colisão elástica, e aqui a colisão é totalmente inelástica.
Então já podemos eliminar a alternativa (b) também. Sabemos que a energia cinética vai diminuir, resta saber se ela vai ser reduzida a zero ou não.
Passo 3
A colisão é totalmente inelástica, então depois dela acontecer as partículas se juntam, formando uma partícula só (que é o nosso sistema).
Uma maneira boa de proceder é assumir que a velocidade final do sistema é zero, assim a energia cinética final seria zero também.
Aí se der alguma inconsistência, tipo um número ao quadrado dando negativo, ou algo assim, vamos saber que a nossa suposição inicial estava errada. E se não der nenhum problema, então nossa suposição vai estar certa, show?
Passo 4
Como a velocidade final do sistema é nula, então o momento linear final também é zero. E o momento linear se conserva, então o momento linear inicial tem que ser zero!
Digamos que as partículas e têm, respectivamente, massas e . O momento linear inicial do sistema vai ser:
E ele tem que dar zero:
Passo 5
Vamos chamar os módulos de e de e , respectivamente.
aponta pra direita, no sentido do eixo e pra cima, no sentido do eixo . Sendo o vetor unitário do eixo , o do eixo , essa equação vai dar:
Passo 6
Comparando os 2 lados, podemos ver que:
Mas as massas e os módulos das velocidades não valem zero, então isso é absurdo! Esse é justamente o tipo de inconsistência que eu falei antes, deu ruim porque a gente assumiu que a velocidade final era zero. Então isso estava errado: a velocidade final não é nula, portanto, a energia cinética é reduzida, mas não a zero.
Momento cultura: Acabamos de fazer uma Reductio ad absurdum (latim para “redução ao absurdo”), que é essa prova por contradição. Agora já dá pra você se gabar com seu professor de física haha ;)
Resposta
Alternativa (a)