Energia Potencial e Conservação de Energia
Sejam dois caminhos diferentes e que começam em um ponto e terminam em um ponto (na figura tem sentido indicado por seta simples e , por seta dupla). Sejam e os trabalhos não nulos realizados por uma força conservativa sobre uma partícula que percorra os caminhos e , respectivamente.
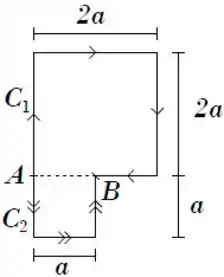
Pode-se afirmar que
(a)
(b)
(c)
(d)
(e)
Passo 1
Cara, a força é conservativa, os pontos de partida e de chegada são os mesmos, então a questão acaba aí! Esses trajetos doidos são só uma pegadinha.
Isso porque uma propriedade, talvez a mais importante das forças conservativas, é o que o trabalho que elas realizam independe da trajetória! É até a definição na Wikipédia! (pode ir lá conferir se não acreditar em mim haha)
Ou seja, não importa se o trajeto foi direto ao ponto, se deu mil voltas ou se passou na China, o trabalho vai ser o mesmo! ;)
Logo,
Resposta
Alternativa (e)