Cinemática Unidimensional
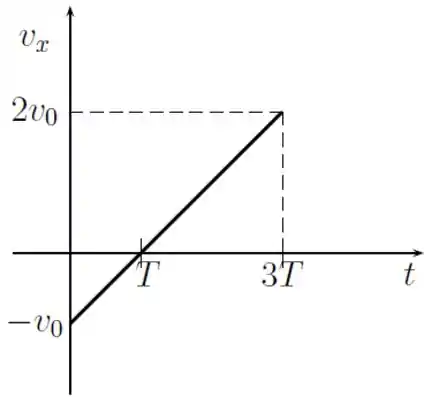
Uma partícula se move ao longo do eixo e o gráfico de sua velocidade em função do tempo em um intervalo de a é o segmento de reta indicado na figura. Podemos afirmar que nesse intervalo de tempo a aceleração da partícula e o seu deslocamento são dados por
(a) e
(b) e
(c) e
(d) e
(e) e
Passo 1
Vamos começar calculando .
A aceleração da partícula é constante, então essa que ele pediu nada mais é que a aceleração média da partícula, então:
Passo 2
A partícula sai no tempo com uma velocidade e chega em com uma velocidade . Então temos
Passo 3
Agora vamos ao deslocamento .
De maneira geral, num MRUV, a posição é dada por:
Nessa questão, partícula segue um MRUV com velocidade inicial e aceleração . E o na verdade não importa! Isso porque ele perguntou o quanto a partícula andou de a , e não em que posição ela está em .
Passo 4
Isso vai ficar mais claro agora! Ele pediu pra gente achar o deslocamento do tempo ao tempo , ou seja:
Os vão cortar e sobra:
Passo 5
Substituindo , vai ficar:
Observação: também podemos achar o deslocamento de outra forma: no gráfico velocidade x tempo, ele é igual à área sob o gráfico!
Resposta
Alternativa (a)