Forças e Leis de Newton, Força de Atrito
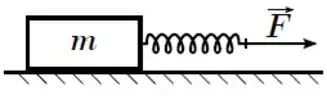
Um bloco de massa é puxado por uma mola ideal em movimento retilíneo sobre uma superfície horizontal com aceleração constante de módulo . O coeficiente de atrito cinético entre o bloco e a superfície é . A elongação da mola é
(a)
(b)
(c)
(d)
(e)
Passo 1
Vamos ver que forças estão atuando no bloco!
Temos, como sempre, a força peso e a força normal da superfície .
E a mola está puxando o bloco pra direita, realizando uma força elástica . Repare que quanto mais a mola é esticada, mais ela vai fazer força no bloco pra voltar à posição de equilíbrio: a força elástica é proporcional à elongação da mola.
Ou seja, essa é aquela que a gente já está acostumado, de módulo
com sendo a constante elástica da mola.
Finalizando, também tem a força de atrito , apontando pra esquerda.
Passo 2
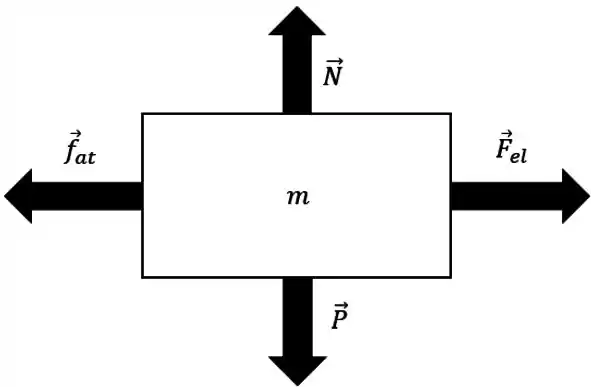
Então o diagrama de forças atuando no bloco é:
Passo 3
O bloco só se move na horizontal, então, pela 2ª lei de Newton:
O bloco está andando pra direita, então em módulo, isso fica:
Passo 4
Já vimos que . E também temos . Portanto, chegamos num sisteminha simples:
Substituindo o valor de na 1ª equação, obtemos
Passo 5
Vamos isolar o , que é o que a gente quer!
Resposta
Alternativa (c)