Um objeto de massa m que pode se mover ao longo do eixo é sujeito a uma força do tipo . No instante de tempo inicial, ele se encontra na posição de equilíbrio em , e recebe um impulso de modo que sua velocidade inicial é > 0. O gráfico que melhor representa como a posição deste objeto varia om o tempo é:
a) 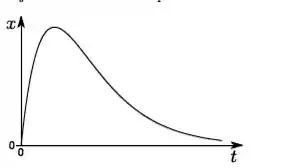
b) 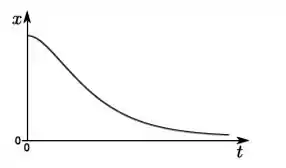
c) 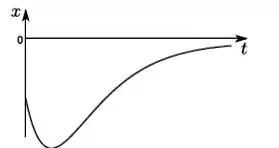
d) 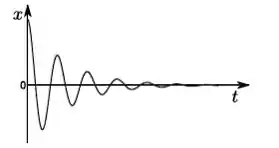
e) 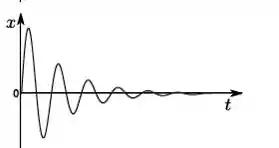
f) 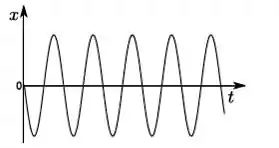
Passo 1
Primeiramente, vamos tentar achar a EDO que representa o movimento.
Através da expressão:
Podemos escrever assim:
Passo 2
Assim:
Dividindo geral por
Passo 3
A ideia agora é a seguinte: Vamos calcular o delta e, a partir dai classificar o tipo de amortecimento. Com isso vamos saber qual gráfico escolher.
Passo 4
Assim, o amortecimento é do tipo crítico.
Checando no nosso capítulo, percebemos que o gráfico referente a esse amortecimento é o que está na alternativa:
a)
Resposta
a)