Uma corda de comprimento esticada tem uma extremidade mantida fixa () e a outra livre . Considere que, na configuração de equilíbrio, a corda se encontra na horizontal ao longo do eixo . Um aluno escreve que os pequenos deslocamentos transversais na direção podem ser representados pelos modos normais:
Onde = 1, 3, 5, ... , e são constantes a serem determinadas das condições iniciais do problema e é a velocidade de propagação da onda na corda. São feitas as seguintes observações sobre a solução apresentada:
- Ela está incorreta, pois não obedece a condição de contorno .
- Os modos pares com = 2, 4, 6,... também deveriam ter sido levados em consideração.
- As condições de contorno para neste problema são as mesmas que uma onda sonora de deslocamento deve obedecer em um tubo de comprimento fechado em uma extremidade e aberto na outra.
- Esta solução não representa uma solução da equação de onda, pois não pode ser escrita na forma, onde é uma constante real e e são funções de uma variável.
São verdadeiras:
- Somente a (III).
- Todas são verdadeiras.
- Nenhuma é verdadeira.
- Somente (I) e (II).
- Somente (I) e (IV).
- Somente (III) e (IV).
- Somente (II) e (IV).
- Somente a (IV)
Passo 1
Vamos analisar uma por uma:
- Essa é falsa: O enunciado nos diz que uma extremidade é mantida fixa( e outra livre Como em a extremidade está livre, não podemos dizer que:
- Não, como estamos lidando com uma corda que é fixa num ponto e livre no outro, podemos associar essa oscilação a uma oscilação de um tubo sonoro fechado em uma extremidade e aberto na outra:
- Como acabamos de ver, podemos associar essa oscilação à oscilação de um tubo desses. Nesse caso, as condições de contorno vão ser as mesmas.
- É claro que essa equação representa uma onda e, logo, é uma solução da equação de onda. Basta a gente perceber que a equação tem o formato da equação de uma onda estacionária.
É uma condição de contorno.
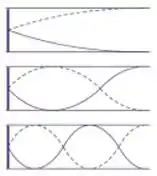
Assim, podemos calcular o comprimento total da corda através da relação:
Ou simplesmente:
Onde é um número ímpar(
Assim, só representamos os modos ímpares mesmo.
Passo 2
Afirmação Verdadeira.
Lembrando que uma onda estacionária pode ser escrita por:
Tanto quanto são soluções da equação de onda.
Resposta
a)