Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Uma onda progressiva em uma corda tem seu perfil de deslocamento descrito por onde é uma função em forma de pulso. Ela incide em uma extremidade fixa da corda em , sendo refletida. Sobre a onda refletida , é correto afirmar que
- É descrita por e o pulso refletido volta sem defasagem.
- É descrita por e o pulso refletido volta om defasagem de 180◦.
- É descrita por e o pulso refletido volta com defasagem de 180◦.
- É descrita por e o pulso refletido volta sem defasagem.
- É descrita por e o pulso refletido volta sem defasagem.
- É descrita por e o pulso refletido volta sem defasagem.
Observação: Acreditamos que existe um erro no enunciado. Usamos ,na resolução,
Passo 1
Bom, imagine essa onda se propagando em um eixo indo de encontro a uma parede localizada a metros da origem desse eixo:
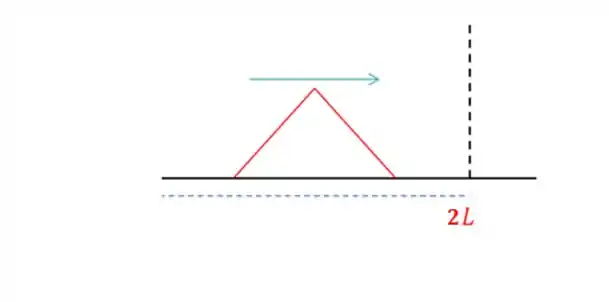
Agora imagine que ela ultrapasse essa parede. Do “ outro lado” da parede, quem domina é um novo referencial: Assim, as distâncias medidas após a parede são medidas em relação a esse referencial.
Podemos dizer que:
Passo 2
Beleza, mas isso tudo foi só uma abstração, afinal de contas, a onda não ultrapassa a parede, ela precisa ser refletida não é?
O, então pensa bem: O que ocorre na realidade, em termos de distâncias, eixos e essas coisas? O que ocorre é que as distâncias após a parede devem ser rebatidas, em relação à parede, no sentido contrário.
Devemos, então, colocar um sinal de menos no novo referencial:
Passo 3
Além disso, como a onda atingiu um ponto, fixo, houve uma reflexão e a onda se inverteu:
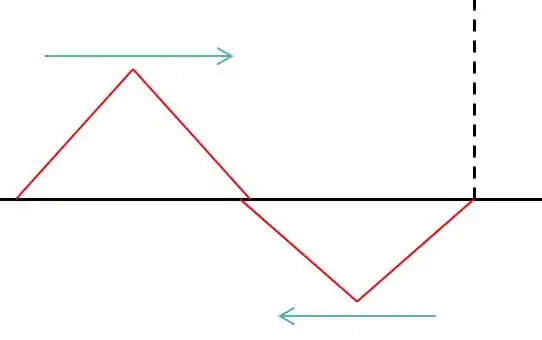
A onda volta com defasagem já que sofreu uma inversão.
Resposta
c)