Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Posição e Fase do MHS

Ver Teoria
Exercício 1212345678910111314151617181920212223242526272829303132333435363738

Enunciado

Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag

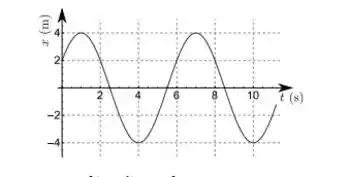
O gráfico a seguir mostra como a posição x de um móvel oscila com o tempo t . A lei horária da posição x ( t ) deste objeto é melhor descrita por

  1. ( 4   m )   c o s   [ ( π 3   s - 1 ) t   -   π 3 ]  
  2. ( 4   m )   c o s   [ ( π 3   s - 1 ) t   +   π 3 ]  
  3. ( 8   m )   c o s   [ ( π 3   s - 1 ) t   -   π 3 ]  
  4. ( 4   m )   c o s   [ ( 2 π 3   s - 1 ) t   -   π 3 ]
  5. ( 8   m )   c o s   [ ( 2 π 3   s - 1 ) t   -   π 3 ]
  6. ( 8   m )   c o s   [ ( 2 π 3   s - 1 ) t   +   π 3 ]
  7. ( 4   m )   s e n   [ ( π 3   s - 1 ) t   +   π 3 ]  
  8. ( 8   m )   s e n   [ ( π 3   s - 1 ) t   –   π 3 ]  

Passo 1

Vamos começar a questão partindo de uma equação genérica assim:

x t = A c o s ω t + φ

Passo 2

Do gráfico, podemos tirar duas informações diretas: A amplitude e o período. Bom, a amplitude é o maior valor de x que aparece no gráfico. Nesse caso, será:

A = 4 m

Passo 3

O período é facilmente descoberto. Vamos prestar atenção no ponto inicial ( t = 0 ,   x = 2 ) ,e vamos ver onde ele vai se repetir pela segunda vez( pois assim um ciclo inteiro já terá sido realizado pelo MHS). Olhando no gráfico, percebemos que isso ocorre em:

t = 6 ,   x = 2 .

Assim, o período é dado por:

T = 6 s

Dai podemos calcular a frequência angular:

ω = 2 π T = 2 π 6 = π 3   r a d / s

Passo 4

Assim. Já temos a função com o formato:

x t = 4 cos ⁡ π 3 t + φ

Agora só basta a gente descobrir a constante de fase.

Pra isso, vamos usar ao ponto inicial, quando t = 0 . Vamos fazer duas análises: A do valor de x naquele ponto e do sinal da velocidade lá.

Vamos primeiro analisar o valor:

x 0 = 2 = 4 cos ⁡ φ → cos ⁡ φ = 1 2

Mas pra esse valor, temos dois ângulos:

φ = π 3   o u   φ = - π 3

Agora precisamos analisar o sinal da velocidade naquele ponto. Pra isso, calculamos a derivada:

d x t d t = v t = - ω A s e n ( ω t + φ )

Para t = 0 :

v 0 = - ω A s e n φ

Mas a velocidade no início é positiva ou negativa? Como a função x ( t ) é crescente naquele ponto, podemos dizer que a velocidade é positiva. Assim, temos que ter:

- ω A s e n φ > 0   → ω A s e n φ < 0 → s e n φ < 0

Ou seja, o seno da fase tem que ser negativo. Logo, o ângulo é:

φ = - π 3

Assim:

x t = 4 cos ⁡ π 3 t - π 3

A resposta é:

a)

Resposta

a)

Exercícios de Livros Relacionados

Qual é a constante de fase do oscilador harmônico cuja função aceleração a(t) aparece na Fig. 15-55 se a função posição x(t) é da forma x = x m c o s ω t + ϕ e a s = 4,0 m / s 2 ?
Recentemente tornou-se possível “pesar” moléculas de DNA medindo a influência de sua massa sobre um nano-oscilador. A figura mostra uma haste fina, retangular e nanométrica, escavada em silicone (dens
A figura ( a ) é um gráfico parcial da função posição x ( t ) de um oscilador harmônico simples com uma frequência angular de 1,20r a d / s ; a figura ( b ) é um gráfico parcial da função velocidade v
A FIGURA Q14.4 mostra um gráfico posição versus tempo para uma partícula em MHS. a. Qual é a constante de fase ϕ 0 ? Explique. b. Qual é a fase da partícula em cada um dos três pontos numerados no grá
A FIGURA Q14.5 mostra um gráfico velocidade versus tempo para uma partícula em MHS. a. Quanto vale a constante de fase ϕ 0 ? Explique. b. Qual é a fase da partícula em cada um dos três pontos, numerad