Um pêndulo simples é formado por um fio ideal de comprimento , ligado a uma massa em uma extremidade e na outra presa a um pino na parede, de modo que ele pode girar livremente, como mostra a figura. Considere conhecida a aceleração da gravidade.

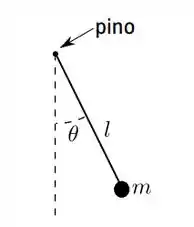
1. Mostre que a energia mecânica (energia cinética + potencial) E deste sistema pode ser escrita como:

Dica: Considere a energia potencial mínima igual a zero no ponto mais baixo da tra jetória do pêndulo.

2. Determine o valor da energia mecânica tal que para o movimento é ilimitado (isto é, o pêndulo pode completar uma volta completa).
3. Aplicando princípios de conservação da energia, obtenha a equação de movimento para as oscilações do pêndulo.
4. Obtenha o período do pêndulo na aproximação de ângulos pequenos (quando, ).
5. Encontre a solução para a equação de movimento deste pêndulo om a aproximação de ângulos pequenos para encontrar o ângulo θ como função do tempo . Considere que, no instante inicial , o pêndulo se encontra na posição de equilíbrio , mas recebe um impulso de modo que a sua velocidade angular inicial é , onde é um parâmetro adimensional conhecido.

Vamos primeiro achar a energia potencial. Ela é dada por:

Mas que é esse

Pela figura abaixo:

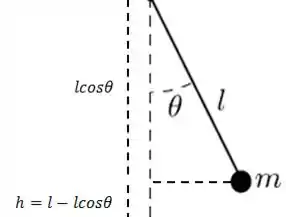
Percebemos que a altura é dada por:

Então, a energia potencial ficará:

E a energia cinética?

Bom, sabemos que ela é dada por:

Podemos escrever de outra forma? Sim, basta a gente se lembrar rapidinho dos movimentos circulares:

Nesse caso, vamos aproximar o movimento do pêndulo por um movimento circular. Nesse caso, quem é

Vai ser o comprimento do pêndulo:

E a velocidade angular? É a variação angular no tempo:

Assim:

Assim:

b):

Para se dar a volta completa, a partícula presa ao pêndulo precisa atingir uma altura máxima:

Que é relativa ao máximo que podemos ter da função:

E para qual valor de conseguimos esse valor?, já que:

Beleza? Pronto, com o valor do ângulo podemos determinar a energia mecânica necessária pra que isso acontece de acordo com a equação que achamos anteriormente:

Obs: Nesse caso, estamos considerando uma energia mínima para que o objeto apenas atinja a altura máxima, ou seja, que ele chegue a essa altura com velocidade nula. Por isso não iremos computar a energia cinética abaixo:

Então é essa a nossa energia mínima:

c)

Bom, a energia mecânica deve se conservar, certo?

Então podemos dizer que:

Assim, derivando a equação abaixo em relação ao tempo:

E essa é a equação de um pêndulo simples.

d):

Para pequenos ângulos, podemos fazer:

Assim:

E obtivemos uma equação padrão de um MHS. Então, a frequência é dada por:

Como a frequência é dada por:

e):

Devemos resolver a equação acima, sabendo que em temos:

e:

Bom, não vamos resolver a equação braçalmente. Sabemos que a solução pra uma EDO de um MHS desses é dada por:

Reescrevendo em termo das variáveis desse problema:

Então a derivada é dada por:

Beleza? Bom, para

Assim:

Lembrando da relação:

Podemos escrever:

Usando a derivada agora:

Comparando com o valor dado:

Assim: