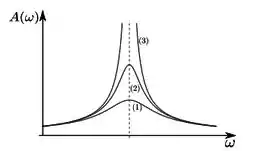
Um objeto de massa m se move no eixo sujeito a uma força horizontal de modo que a equação de movimento é dada por , onde ≥ 0, > 0 e > 0. A amplitude da solução particular desta equação varia com ω de acordo com o que mostra a figura em três situações correspondentes a valores diferentes e , tal que ≫ .

É INCORRETO afirmar que:

a) Quanto maior o valor de , maior a amplitude máxima da curva correspondente.

b) O amortecimento é maior na curva (1).

c) A frequência de ressonância é a mesma para as três curvas.

d) A curva (3) corresponde ao aso sem amortecimento.

e) Para ω ≫ , a solução particular é defasada de π em relação à força externa.

a) Será que quanto maior for a frequência maior será a amplitude? Claro que não, como vimos no nosso capítulo, a amplitude será maior quanto mais próxima for da frequência de ressonância( na expressão,

Então essa é a incorreta.

b) Olhando a expressão do início da questão, você vai perceber que quanto maior for o amortecimento(, maior será o denominador e menor será a razão, logo, menor será a amplitude. Então, a afirmação está correta, já que a curva 1 tem a menor amplitude.

c) Verdade. Como podemos ver no gráfico, os picos das três curvas, as máximas amplitudes, estão alinhados. E como é nesse ponto que ocorre a ressonância, podemos dizer que, sim, a frequência de ressonância é a mesma para todas as curvas.

Correta, então!

d) Sim, caso não tenhamos amortecimento, vamos ter a expressão:

Se fizermos tender a a amplitude vai tender ao infinito. É isso que o gráfico dessa curva mostra.

Correta!

e) Sim!!! Vamos pensar no caso em que não há dissipação. Pela nossa teoria, temos que a fase da solução particular será:

A situação dessa letra se enquadra no segundo caso acima. Assim, a solução particular será dada por:

Por causa dessa fase, podemos dizer que a solução está defasada da força externa sim.

Opção correta também!