P3 de Física 2 da UFRJ - 2018.2

Um oscilador levemente amortecido () perde 10% de sua energia média inicial em . De que percentual sua energia terá caído em ?

1. 80%
2. 20%
3. 81%
4. 19%

Se a temperatura de um gás ideal se duplica mantendo a pressão constante, ao atingir o equilíbrio térmico a velocidade quadrática média das moléculas:

1. Cresce por um fator 4.
2. Permanece constante.
3. Cresce por um fator .
4. Cresce por um fator 2.
5. Diminui por um fator 2.

Dez trompetistas estão tocando a mesma nota musical com intensidades sonoras iguais. A intensidade sonora medida por um ouvinte na plateia é de 40 decibéis. Suponha que o ouvinte esteja a uma distância grande dos trompetistas, de forma que a diferença de posição entre eles possa ser desprezada. Se nove deles pararem de tocar, a nova intensidade sonora medida será de:

1. 20 decibéis.
2. 40 decibéis.
3. 30 decibéis.
4. 10 decibéis.
5. 4 decibéis.

Uma corda tem densidade linear de massa e está submetida a uma tração . Para aumentarmos o comprimento das ondas periódicas nesta corda sem modificar o período, a ação correta é:

1. Aumentar a amplitude da onda.
2. Aumentar .
3. Aumentar
4. Aumentar o número de onda.
5. Aumentar a frequência.

Quais das seguintes afirmativas estão corretas?

I. A frequência num movimento harmônico simples é independente da amplitude.

II. O movimento de oscilação de um pêndulo é em geral harmônico simples

III. Na ressonância o deslocamento no regime estacionário de um oscilador forçado está em fase com a força externa , resultando em uma absorção máxima de energia.

IV. Um sistema amortecido atinge o equilíbrio mais rapidamente quando o fator de amortecimento estiver próximo de seu valor crítico

1. II e III
2. I e II
3. III e IV
4. I, II, III e IV
5. I e IV

Um objeto preso em uma mola realiza um movimento harmônico simples de amplitude . Quando o objeto se encontra a da posição de equilíbrio, qual fração de sua energia total é energia potencial?

1. Dois terços.
2. Um terço.
3. Metade.
4. Um quarto.
5. Três quartos.

Um oscilador amortecido forçado, com , é colocado para oscilar a partir de duas condições iniciais distintas denominadas . O resultado dessas oscilações é graficado como versus t na figura abaixo.

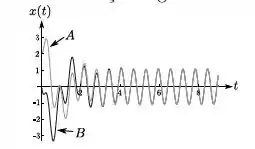
Marque a afirmativa correta:

1. As oscilações de no regime estacionário são iguais pois não dependem das condições iniciais.
2. As condições iniciais para A são .
3. As condições iniciais para são
4. As soluções transientes de são iguais pois não dependem das condições iniciais.
5. Somente está próximo da ressonância.

Um pêndulo de comprimento , inicialmente em repouso na sua posição de equilíbrio, recebe um impulso que lhe comunica instantaneamente uma velocidade angular no sentido anti-horário. Seja a frequência angular das oscilações. A função que descreve corretamente seu movimento, supondo pequenas oscilações, é:

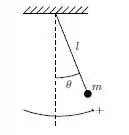
Uma criança coloca um pouco de areia dentro de uma garrafa de refrigerante vazia e a põe para boiar em um tanque com água. Podemos supor que a garrafa tem seção reta uniforme de área , sendo muito menor que a área do tanque, de forma que o movimento da água do tanque possa ser desprezado. A massa total da garrafa, incluindo a areia, vale . A densidade da água é . No equilíbrio, a parte submersa da garrafa tem comprimento . A criança força a garrafa para baixo uma pequena distância além da posição de equilíbrio, e a solta. Considerando que a garrafa tenha apenas movimento vertical, a frequência angular de suas oscilações em torno do equilíbrio vale:

Uma corda de comprimento tem o extremo em fixo e o extremo emlivre. Quando vibra em um de seus modos normais, um ponto da corda num ventre oscila dez vezes por segundo e seu deslocamento atinge o valor máximo de . A distância entre ventres adjacentes vale .

a) Determine o comprimento de onda bem como a velocidade de propagação das ondas nesta corda.

b) Faça um esboço do perfil da corda neste modo de vibração, no instante em que todos os seus pontos têm deslocamento máximo. Indique claramente a posição de cada nó.

c) Escreva as expressões para a velocidade transversal dos pontos extremos da corda. Considere para a constante de fase da parte temporal de .