Um oscilador amortecido forçado, com , é colocado para oscilar a partir de duas condições iniciais distintas denominadas . O resultado dessas oscilações é graficado como versus t na figura abaixo.

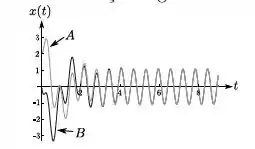
Marque a afirmativa correta:

1. As oscilações de no regime estacionário são iguais pois não dependem das condições iniciais.
2. As condições iniciais para A são .
3. As condições iniciais para são
4. As soluções transientes de são iguais pois não dependem das condições iniciais.
5. Somente está próximo da ressonância.

Vamos analisar uma por uma.

1. As oscilações de no regime estacionário são iguais pois não dependem das condições iniciais.

Tá certa e é a resposta. Lembra que no MHA o movimento vai pra zero depois de um tempo? Isso quer dizer que as condições iniciais já não importam depois de um tempo, ficando só a solução particular do sistema, que é a da força externa.

2. As condições iniciais para A são .

Tá errada. Pelo gráfico, para A, e . Como é a derivada, ela só é zero nos pontos de máximo e mínimo (quer dizer, nas cristas e cavados das ondas).

3. As condições iniciais para são

Tá errada pelo mesmo motivo. Para B, , mas .

4. As soluções transientes de são iguais pois não dependem das condições iniciais.

Essa tem nada a ver. Pelo gráfico, as soluções transientes (aquelas que se modificam, onde esse gráfico tá zoadaço, logo no início) são bem diferentes pra A e B. Elas só ficam iguais (coincidentes) no final, no regime estacionário.

5. Somente está próximo da ressonância.

Tá errada porque, como a ressonância é amplitude máxima, nenhum dos dois está próximo da ressonância.

Então resposta letra A.