Uma corda de comprimento tem o extremo em fixo e o extremo emlivre. Quando vibra em um de seus modos normais, um ponto da corda num ventre oscila dez vezes por segundo e seu deslocamento atinge o valor máximo de . A distância entre ventres adjacentes vale .
a) Determine o comprimento de onda bem como a velocidade de propagação das ondas nesta corda.
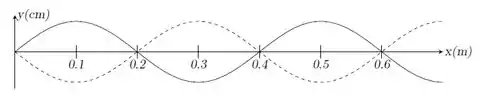
b) Faça um esboço do perfil da corda neste modo de vibração, no instante em que todos os seus pontos têm deslocamento máximo. Indique claramente a posição de cada nó.
c) Escreva as expressões para a velocidade transversal dos pontos extremos da corda. Considere para a constante de fase da parte temporal de .
Passo 1
a) A distância entre dois ventres (ou entre dois nós) consecutivos equivale a meio comprimento de onda. Então:
Ele disse que um ponto da corda num ventre oscila 10 vezes por segundo. Isso quer dizer que .
Como já temos a frequência e o comprimento de onda, podemos achar a velocidade:
Passo 2
b) Repara que: como e , vai caber uma vez nessa corda e vão sobrar . Ou seja, vão sobrar . Então podemos dizer que:
Vamos lembrar que a equação da onda é:
Nos instantes em que os deslocamentos forem máximos, deveremos ter:
Então:
Como ele disse que a amplitude é de :
Os nós ocorrem em pontos em que , sendo um número inteiro.
Ou seja:
Passo 3
c) O ponto corresponde a um nó. Como nos nós a velocidade é zero:
O ponto corresponde a um ventre, que vibra com amplitude máxima, portanto:
Logo, derivando:
Sabemos que . Podemos calcular a frequência angular:
Substituindo:
Usando :
Resposta
a),
b)
c)