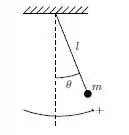
Um pêndulo de comprimento , inicialmente em repouso na sua posição de equilíbrio, recebe um impulso que lhe comunica instantaneamente uma velocidade angular no sentido anti-horário. Seja a frequência angular das oscilações. A função que descreve corretamente seu movimento, supondo pequenas oscilações, é:
Passo 1
Inicialmente, sabemos que a equação do MHS é descrita como:
E a velocidade (derivando):
Mas como no instante , instante em que ele recebeu o impulso, o ângulo é igual a (pêndulo na posição vertical), devemos ter:
Por isso:
Ou:
Vamos descobrir qual dos dois valores usar! Quando a velocidade angular é positiva. Então:
Pra isso ser verdade, . Então:
E a equação vai ficar:
E a velocidade como:
Passo 2
Show, agora que achamos as equações do MHS, temos que achar o valor de, porque ele não aparece na equação. E como vamos fazer isso?
Pra isso, você tem que tá ligadx que a velocidade angular quando o pêndulo passa pela posição mais baixa vai ser máxima. Porque nesse ponto temos energia potencial mínima, logo, teremos energia cinética máxima. Sacou?
E a velocidade máxima é a amplitude da velocidade. Ou seja:
Mas como essa velocidade máxima é a velocidade no ponto mais baixo, vamos ter:
Que é a velocidade no ponto mais baixo, imediatamente após o impulso.
Então podemos isolar :
E substituindo na equação do MHS:
Passo 3
Puts, nossa resposta não bateu. E agora?
Vamos abrir esse cosseno aí:
Substituindo:
Só uma observação:

Você pode tá pensando: a energia cinética leva em consideração a velocidade tangencial, , não a velocidade angular . Acontece que como:
A velocidade vai ser máxima quando for máxima, e vice-versa. Ou seja, nossa análise está corretíssima!
Fim da observação.
Resposta
Letra A