P3 de Física 2 da UFRJ - 2019.1

Uma mola ideal, de comprimento relaxado e constante elástica k tem um de seus extremos presos ao teto de um laboratório. Para um pequeno bloco de massa é conectado à extremidade livre da mola e o sistema permanece em equilíbrio na posição num eixo cuja origem corresponde ao ponto em que a mola não tem deformação, como mostrado na figura (). A uma altura abaixo desta posição há um dispositivo sensível ao toque que acende uma lâmpada cada vez que é tocado pelo bloco como pode ser visto na figura (). Em você encosta o bloco no dispositivo e o libera a partir do repouso. Despreze quaisquer forças dissipativas no sistema, utilize o eixo da figura () e JUSTIFIQUE todas as respostas. Suponha a gravidade conhecida.

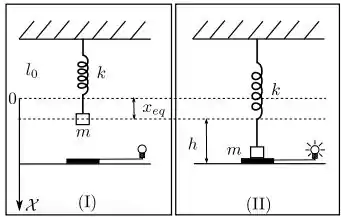
Responda aos QUATRO itens abaixo:

1. Calcule .

2. Obtenha a equação diferencial do movimento do bloco para .

3. Considere, APENAS NESTE ITEM, que . Para que valor da constante elástica da mola a lâmpada acende em intervalos de tempo de segundo?

4. Determine a função de movimento do bloco para

USANDO AS CONDIÇÕES INICIAIS.

Uma corda de comprimento tem massa e está submetida a uma tração , com o extremo em preso a um suporte numa parede. Uma onda é produzida nesta corda ao movimentar-se seu extremo em num movimento harmônico com um período de . No instante esta extremidade da corda passava por com velocidade .

c) Após um longo intervalo de tempo a onda terá percorrido a corda várias vezes, ao se refletir nos extremos, formando uma onda estacionária. Supondo que a amplitude das oscilações em possa ser desprezada (por ser pequena em comparação com a amplitude final da onda formada), faça um esboço do perfil da corda num instante tal que . Deixe claro a localização dos nós e dos ventres.

Onde aplicável, a resposta pode ficar em função de .

Uma corda de comprimento tem massa e está submetida a uma tração , com o extremo em preso a um suporte numa parede. Uma onda é produzida nesta corda ao movimentar-se seu extremo em num movimento harmônico com um período de . No instante esta extremidade da corda passava por com velocidade .

a) Calcule a velocidade de propagação , a frequência angular e o comprimento de onda da onda formada na corda.

b) Escrevendo a função de onda na forma , determine a amplitude e a constante de fase desta onda, antes que ela atinja o outro extremo em .

Onde aplicável, a resposta pode ficar em função de .

Uma massa suspensa por um fio está em repouso na posição de equilíbrio quando em recebe um impulso que faz com que se mova no sentido anti-horário (positivo), atingindo um ângulo máximo de . Suas oscilações subsequentes levam dois segundos para completar cada ciclo. A função que descreve corretamente seu movimento é:

(a)

(b)

(c)

(d)

(e)

A gráfico abaixo mostra o deslocamento do equilíbrio de uma onda transversal nos instantes (linha tracejada) e (linha contínua). Durante este intervalo o máximo que estava em cm moveu-se para . A frequência das oscilações desta onda vale:

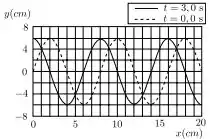
(a)

(b)

(c)

(d)

Um observador parado no acostamento de uma rodovia vê o carro da polícia passar em perseguição a um carro suspeito. A velocidade do carro da polícia é maior que a do outro. Sendo a frequência da sirene do carro da polícia quando em repouso, a frequência percebida pelo observador enquanto os carros se afastam e a frequência percebida pelos ocupantes do carro suspeito, podemos ordená-las da seguinte forma:

(a)

(b)

(c)

(d)

A posição como função do tempo para um oscilador levemente amortecido é descrita por , com todas as grandezas em unidades . A energia média inicial acumulada neste oscilador terá se reduzido a metade em que intervalo de tempo ?

(a)

(b)

(c)

(d)

(e)

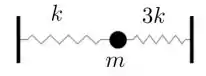
Uma certa massa m está presa a duas molas de constantes elásticas k e 3k, conforme a figura. O período de oscilação do movimento dessa massa é dado por:

(a)

(b)

(c)

(d)

(e)

(f)

Inicialmente a uma certa temperatura um bloco de densidade e coeficiente de dilatação volumétrica está parcialmente submerso em um líquido de densidade volumétrica e coeficiente de dilatação volumétrica . Considere que nesta situação a razão entre o volume submerso e o volume total do bloco seja . Após uma variação de temperatura , ambos o bloco e o líquido irão se dilatar de forma que o bloco continua parcialmente submerso. A nova razão entre o volume submerso e o volume total do bloco será:

(a)

(b)

(c)

(d)

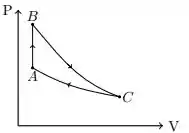
A figura mostra o esboço de um diagrama para um gás ideal com um ciclo reversível formado por uma transformação a volume constante, uma transformação isotérmica e uma transformação adiabática, não necessariamente nesta ordem. O ciclo é percorrido no sentido .

Considere as seguintes afirmações:

I. O calor é absorvido pelo gás na etapa e rejeitado na etapa .

II. O calor total transferido é negativo e o ciclo descreve um refrigerador.

III. A variação da entropia do gás a cada ciclo completo é nula.

IV. A variação da energia interna do gás, em módulo, é maior na etapa do que na etapa .

V. O calor é absorvido pelo gás na etapa e rejeitado na etapa .

As afirmativas corretas são:

(a) e .

(b) e .

(c) e .

(d) , e .

(e) , e .