Uma mola ideal, de comprimento relaxado e constante elástica k tem um de seus extremos presos ao teto de um laboratório. Para um pequeno bloco de massa é conectado à extremidade livre da mola e o sistema permanece em equilíbrio na posição num eixo cuja origem corresponde ao ponto em que a mola não tem deformação, como mostrado na figura (). A uma altura abaixo desta posição há um dispositivo sensível ao toque que acende uma lâmpada cada vez que é tocado pelo bloco como pode ser visto na figura (). Em você encosta o bloco no dispositivo e o libera a partir do repouso. Despreze quaisquer forças dissipativas no sistema, utilize o eixo da figura () e JUSTIFIQUE todas as respostas. Suponha a gravidade conhecida.
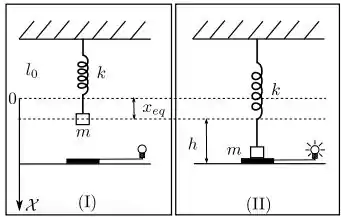
Responda aos QUATRO itens abaixo:
1. Calcule .
2. Obtenha a equação diferencial do movimento do bloco para .
3. Considere, APENAS NESTE ITEM, que . Para que valor da constante elástica da mola a lâmpada acende em intervalos de tempo de segundo?
4. Determine a função de movimento do bloco para
USANDO AS CONDIÇÕES INICIAIS.
Passo 1
(a)
Na posição de equilíbrio, temos a seguinte situação:
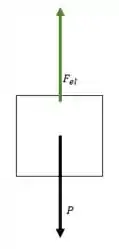
Bom, e na posição de equilíbrio a força resultante sobre o bloco é nula, dessa forma:
Passo 2
(b)
Bom, para encontrarmos a equação diferencial do movimento, vamos olhar para equação da força resultante atuando sobre o bloco! As forças que atuam sobre o bloco são seu peso e a força exercida pela mola, em sentidos contrários, certo? Pela segunda Lei de Newton, temos:
Lembrando que podemos escreve a aceleração () como () e substituindo as forças elástica e peso:
Passando para o outro lado e dividindo tudo por :
Pronto, essa é a equação diferencial do movimento!! Onde é a frequência natural de oscilação do sistema.
DICA: para achar a equação diferencial de algum movimento, tenta olhar para a segunda Lei de Newton e fazer essas continhas!! Ela ajuda muito 😊
Passo 3
(c)
O período no qual a lâmpada acende é igual ao período de oscilação do bloco. Já que, para tocar no dispositivo, ela deve descer tuuudo e depois subir, completando o movimento de oscilação! Assim, temos:
O problema quer que a lâmpada acenda num intervalo de , logo . E, elevando a equação toda ao quadrado:
Passo 4
(d)
A função de movimento é justamente a solução da equação diferencial que achamos na letra (b)! E vai ter essa cara ó:
onde é uma solução particular da equação diferencial. Além disso, podemos lembra da teoria que a solução homogênea de um movimento harmônico qualquer é dado pelo movimento harmônico simples, ou seja, pode ser escrita na forma:
Onde e são constantes a serem determinadas a partir das condições iniciais.
Olhando pra equação da letra (b):
Vemos que o termo não homogêneo da equação diferencial é constante (é a gravidade ali do lado esquerdo da igualdade). Então, é só colocar como solução particular da edo (), uma constante qualquer. Então, substituindo na edo que :
Assim, a solução geral do problema fica:
Passo 5
Agora vamos achar o valor das constantes usando as condições iniciais do problema!
No enunciado ele diz que em você encosta o bloco no dispositivo e o libera a partir do repouso. Logo:
Nossa solução , então .
Com isso:
Bom, isso não nos diz muita coisa ainda. Mas calma, vamos ver se a equação da velocidade do movimento nos diz alguma coisa.
Como o bloco é liberado do repouso:
E, derivando em relação a :
Como vimos:
Isso implica que, já que é diferente de zero!
Substituindo em , que achamos agora há pouco:
Desta forma, a solução do problema fica escrita como:
Lembrando que .
Amém! Acabamos hahaha deu tudo certo!
Resposta
- , onde