Uma corda de comprimento tem massa e está submetida a uma tração , com o extremo em preso a um suporte numa parede. Uma onda é produzida nesta corda ao movimentar-se seu extremo em num movimento harmônico com um período de . No instante esta extremidade da corda passava por com velocidade .
c) Após um longo intervalo de tempo a onda terá percorrido a corda várias vezes, ao se refletir nos extremos, formando uma onda estacionária. Supondo que a amplitude das oscilações em possa ser desprezada (por ser pequena em comparação com a amplitude final da onda formada), faça um esboço do perfil da corda num instante tal que . Deixe claro a localização dos nós e dos ventres.
Onde aplicável, a resposta pode ficar em função de .
Passo 1
Bom, da teoria, nós temos que numa onda estacionária:
Onde é a frequência do enésimo modo de vibração.
Com isso, achamos qual o modo de vibração da onda!
O valor de nós temos pelo enunciado, . Então, falta acharmos o valor de e !
Passo 2
Primeiro, vamos achar a velocidade. Para isso, podemos usar a fórmula da velocidade numa corda:
Onde , pois trata-se da densidade linear da corda. Substituindo na fórmula:
Passo 3
Show! Agora, vamos para .
O enunciado nos disse que e , logo:
Passo 4
Beleza! Agora, podemos achar o valor de , que simboliza nosso modo de vibração:
Opa, então nossa onda está no segundo modo de vibração!
Passo 5
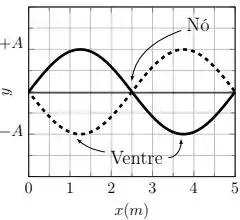
Como , temos essa situação:

E esse já pode ser um esboço da nossa onda!!
Sendo assim, o comprimento de onda () é exatamente o tamanho da própria corda, ou seja: .
Como podemos ver no nosso esboço, temos um nó no meio da corda, ou seja, um nó em . E dois ventres, um antes e outro depois do nó, bem no meio do caminho entre o nó e as extremidades. Logo, eles estão: um metade de antes e outro metade de depois do nó, ou seja, e .
Desenhando isso tudo:
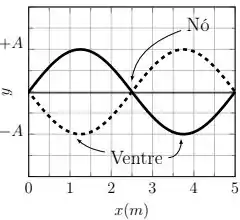
Resposta