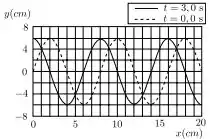
A gráfico abaixo mostra o deslocamento do equilíbrio de uma onda transversal nos instantes (linha tracejada) e (linha contínua). Durante este intervalo o máximo que estava em cm moveu-se para . A frequência das oscilações desta onda vale:
(a)
(b)
(c)
(d)
Passo 1
Pela leitura do gráfico, tiramos que o comprimento dessa onda (, distância entre os dois máximos dela) vale . E sabemos que:
Além disso, o enunciado nos disse que essa onda se deslocou em , logo .
Jogando isso na fórmula da frequência:
OBS.: Repare que os “centímetros” se cortam, por isso não precisamos passar tudo para metro 😊
Resposta
Alternativa (c).