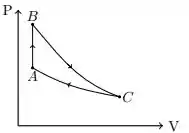
A figura mostra o esboço de um diagrama para um gás ideal com um ciclo reversível formado por uma transformação a volume constante, uma transformação isotérmica e uma transformação adiabática, não necessariamente nesta ordem. O ciclo é percorrido no sentido .

Considere as seguintes afirmações:

I. O calor é absorvido pelo gás na etapa e rejeitado na etapa .

II. O calor total transferido é negativo e o ciclo descreve um refrigerador.

III. A variação da entropia do gás a cada ciclo completo é nula.

IV. A variação da energia interna do gás, em módulo, é maior na etapa do que na etapa .

V. O calor é absorvido pelo gás na etapa e rejeitado na etapa .

As afirmativas corretas são:

(a) e .

(b) e .

(c) e .

(d) , e .

(e) , e .

Show, por eliminação, só temos duas opções: e ou e .

Então, vamos ver a :

“A variação da energia interna do gás, em módulo, é maior na etapa do que na etapa .”

A variação da energia interna só depende da variação de temperatura do processo. Isso dá para ser visto na fórmula:

Já que é constante.

No processo , temos que a variação de temperatura é:

No processo , a variação de temperatura é:

Só que , já que o processo é isotérmico. Então:

Opaaaa, como queremos o módulo da variação da energia em interna e, em módulo, a variação das temperaturas é igual, a variação das energias internas também será igual!! E essa afirmativa se torna falsa!

Outra forma de reconhecer isso é ver que, nos ciclos . E, como no processo não temos variação de energia interna, já que não tem variação de temperatura, as variações das energias internas dos processos e devem se anular para que . Ou seja:

E, então: