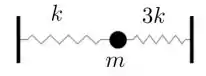
Uma certa massa m está presa a duas molas de constantes elásticas k e 3k, conforme a figura. O período de oscilação do movimento dessa massa é dado por:
(a)
(b)
(c)
(d)
(e)
(f)
Passo 1
Vamos olhar com carinho: se deslocarmos o bloco para direita, por exemplo, a mola da direita irá empurrar o bloco com uma força e a mola da esquerda irá puxar o bloco com uma força (ambas as forças serão negativas porque estarão no sentido contrário a esse movimento). Assim, a força Total será:
Que funciona como um sistema massa-mola com uma constante . Como a frequência é dada por :
Passo 2
Podemos relacionar o período e a frequência angular por:
Resposta
Alternativa (d).
Exercícios de Livros Relacionados
Na figura, duas molas são ligadas entre si e a um bloco de massa 0,245k g que oscila em um piso sem atrito. As duas molas possuem uma constante elástica k = 6430N / m . Qual é a frequência das oscilaç
(a) Estime o período natural de oscilações por balançar seus braços quando você anda, quando suas mãos estão vazias. (b) Agora estime o período natural de oscilação quando você está carregando uma mal
Com um bloco de massa m e duas molas, de constantes elásticas k 1 e k 2 , montam-se dois arranjos indicados nas Figuras (a) e (b). Calcule as respectivas frequências angular ω a e ω b de pequenas osci
Mostre que, nas situações mostradas na figura, o corpo oscila com uma frequência f = 1 2 π k e f m , onde k e f é dado por (a) k e f = k 1 + k 2 e (b) 1 / k e f = 1 / k 1 + 1 / k 2 . Dica: Determine a
Durante um terremoto, um piso horizontal oscila horizontalmente em um movimento harmônico simples aproximado. Suponha que ele oscile em uma única frequência, com 0,80s de período. (a) Após o terremoto