PF de Física 2 da UFRJ - 2017.1

Considere as seguintes afirmações a respeito de ondas sonoras.

I. Batimentos ocorrem quando duas ondas cujas frequências são múltiplos inteiros uma da outra se sobrepõem.

II. Pode existir um som cujo nível de intensidade sonora seja −10 dB.

III. A propagação das ondas sonoras no ar se dá por um processo adiabático.

Quais destas propriedades são corretas?

(a) Nenhuma.

(b) Apenas (I).

(c) Apenas (II).

(d) Apenas (III).

(e) (I), (II) e (III).

(f) Apenas (I) e (II).

(g) Apenas (I) e (III).

(h) Apenas (II) e (III).

Um oscilador harmônico simples tem amplitude , atinge velocidade máxima de e

possui aceleração máxima . Num dado instante de tempo, qual das opções abaixo pode

representar sua posição, sua velocidade e sua aceleração, respectivamente?

(a) , , .

(b) , , .

(c)

(d) , , .

(e) , , .

(f) , , .

(g) , , .

(h) Nenhuma das alternativas anteriores.

Consideremos uma mola com 2 constantes elásticas: , quando é esticada e , quando comprimida, tal que:

Suponha que esta mola seja presa a um bloco de massa que pode oscilar sobre uma superfície horizontal sem atrito. O período de oscilação do sistema é:

7. Nenhuma das alternativas acima.

No interior de uma solução de sais em líquido, a densidade da solução varia com respeito à altitude. Numa solução deste tipo e em equilíbrio com o campo gravitacional na superfície da terra, a pressão varia com a profundidade h da seguinte forma: . Qual

a expressão para a densidade como função da profundidade?

(a) .

(b) .

(c)

(d)

(e)

(f)

(g) .

Um pesquisador quer estudar o comportamento termodinâmico de sólidos através de uma simulação de computador. Ele modela um sólido como uma rede cristalina de N = 1 bilhão de átomos ligados aos seus vizinhos por molas ideais. Contudo, seus “átomos” estão restritos a um plano (ou seja, a simulação é inteiramente bidimensional). Para testar se sua simulação está bem feita, ele calcula a energia interna do seu sólido. Qual o valor que ele espera encontrar?

(a) = (1/2)NT.

(b) = NT.

(c) = (3/2)NT.

(d) = (5/2)NT.

(e) = 2NT.

(f) = 3NT.

(g) = (7/2)NT.

Uma fonte sonora emite uma onda esférica de modo que um pequeno detector, situado a uma distância da fonte, mede uma intensidade sonora de . Nessa posição, a amplitude da onda de pressão sonora é . Para uma distância do centro de emissão, esse mesmo detector mede uma intensidade e amplitude de pressão , respectivamente iguais a

(a) .

(b) .

(c) .

(d .

(e) .

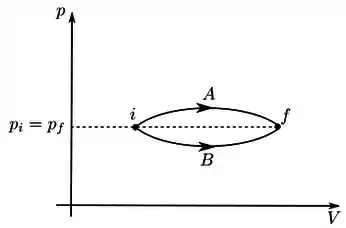
Considerando o processo mostrado no diagrama pxV de um gás ideal, qual é a opção correta a respeito do calor trocado nos processos A e B e os valores da entropia nos estados inicial i e final f?

Um torcedor em um vagão do trem em direção ao maracanã assopra uma corneta vuvuzela gerando uma nota a uma frequência de 235 Hz. Sabendo que a velocidade do vagão é de 20 m/s e a velocidade do som é de 340 m/s, podemos dizer que a frequência do som recebido por um passageiro encostado na parede da estação Maracanã e a frequência do som refletido pela parede até a fonte são dadas respectivamente por:

(a) ∼ 250 Hz e ∼ 221 Hz.

(b) ∼ 222 Hz e ∼ 235 Hz.

(c) ∼ 235 Hz e ∼ 247 Hz.

(d) ∼ 250 Hz e ∼ 235 Hz.

(e) ∼ 222 Hz e ∼ 209 Hz.

(f) ∼ 222 Hz e ∼ 264 Hz.

(g) ∼ 250 Hz e ∼ 264Hz.

(h) Nenhuma das anteriores.

Partindo de um estado de equilíbrio (), um gás ideal sofre uma expansão realizando

trabalho W. Se este processo for isotérmico, o gás atinge o estado (), caso este seja

adiabático, o estado final é (). Considerando que a mesma quantidade de trabalho

foi realizada em ambos os processos, pode-se afirmar que

Um sifão é usado para retirar um fluido incompressível de um recipiente aberto, como mostra a figura. A área de seção reta A é constante ao longo do tubo e muito menor que a área da superfície livre do fluido no recipiente.

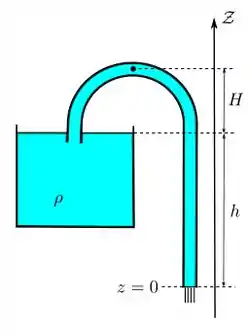
(a) Calcule a velocidade do fluido na saída do sifão, no regime estacionário.

(b) Calcule a pressão no ponto mais alto do sifão.

(c) Calcule o valor máximo da distância (H + h) para que o sifão funcione (o fluido saia na extremidade do tubo).