Um sifão é usado para retirar um fluido incompressível de um recipiente aberto, como mostra a figura. A área de seção reta A é constante ao longo do tubo e muito menor que a área da superfície livre do fluido no recipiente.
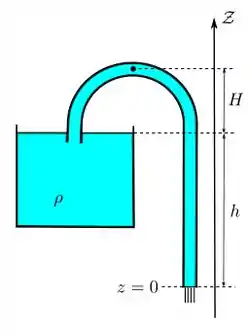
(a) Calcule a velocidade do fluido na saída do sifão, no regime estacionário.
(b) Calcule a pressão no ponto mais alto do sifão.
(c) Calcule o valor máximo da distância (H + h) para que o sifão funcione (o fluido saia na extremidade do tubo).
Passo 1
Questãozinha de hidrodinâmica, que só tem duas fórmulas, o princípio da continuidade
E a equação de Bernoulli
Desde que usada em ponto na mesma linha de corrente, como a exemplificada abaixo em vermelho.
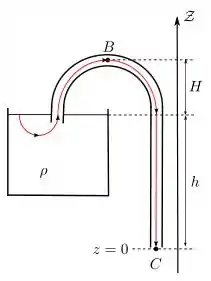
Como a questão diz que a área do tubo () é muito menor do que a área da superfície livre (), pelo princípio da continuidade
Então consideramos a velocidade na área livre como praticamente nula .
Passo 2
a) Queremos a velocidade de saída do sifão, para isso podemos usar Bernoulli entre o ponto de saída do líquido (Ponto C) e a superfície livre do líquido (Ponto A).
Temos que , , e como ambos os pontos estão em contato direto com a atmosfera, então :
Passo 3
b) Queremos a pressão no ponto B. Podemos aplicar Bernoulli entre a A e B, por exemplo.
, , , . E como dentro do tubo as áreas são iguais , então pelo princípio da continuidade
Passo 4
c) Para que o fluido saia na extremidade do tubo, temos que ter pressão no ponto mais alto para que haja força para “puxar” o líquido. Matematicamente: