Partindo de um estado de equilíbrio (), um gás ideal sofre uma expansão realizando
trabalho W. Se este processo for isotérmico, o gás atinge o estado (), caso este seja
adiabático, o estado final é (). Considerando que a mesma quantidade de trabalho
foi realizada em ambos os processos, pode-se afirmar que
Passo 1
Um expansão acontece em ambos os casos, então trabalho é realizado pelo sistema, podemos considerar esse trabalho positivo () se usarmos a primeira lei da termodinâmica como
No processo isotérmico não temos variação de temperatura, então
Já processo adiabático, como , então,
A energia interna diminui! Ou seja, a temperatura diminui: .
Já podemos dizer que
Passo 2
Para verificar a pressão e volume, podemos lembrar que no processo isotérmico, temos a relação
Já no processo adiabático, a relação é um pouco diferente,
Se colocarmos isso no diagrama PV, devido ao expoente no volume, a curva do processo adiabático é bem mais inclinada do que a do processo isotérmico.
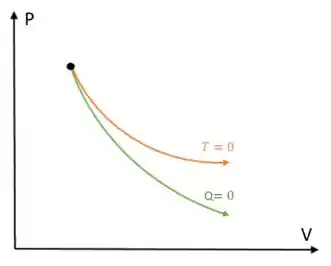
Passo 3
O trabalho,
É justamente a área embaixo da curva. Como , então as duas áreas abaixo das curvas tem que ser iguais. Como a adiabática está abaixo da isotérmica, para igualar as áreas, ela precisa ir até volumes maiores.
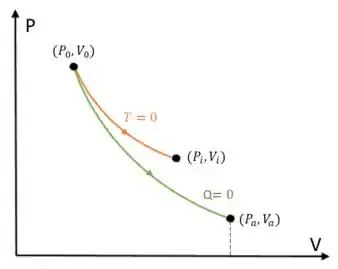
Podemos tirar do gráfico que