Um torcedor em um vagão do trem em direção ao maracanã assopra uma corneta vuvuzela gerando uma nota a uma frequência de 235 Hz. Sabendo que a velocidade do vagão é de 20 m/s e a velocidade do som é de 340 m/s, podemos dizer que a frequência do som recebido por um passageiro encostado na parede da estação Maracanã e a frequência do som refletido pela parede até a fonte são dadas respectivamente por:
(a) ∼ 250 Hz e ∼ 221 Hz.
(b) ∼ 222 Hz e ∼ 235 Hz.
(c) ∼ 235 Hz e ∼ 247 Hz.
(d) ∼ 250 Hz e ∼ 235 Hz.
(e) ∼ 222 Hz e ∼ 209 Hz.
(f) ∼ 222 Hz e ∼ 264 Hz.
(g) ∼ 250 Hz e ∼ 264Hz.
(h) Nenhuma das anteriores.
Passo 1
Questãozinha de efeito Doppler.
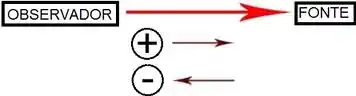
Onde O é o observador e F é a fonte sonora.
Ah, mas tem um monte de sinal aí, como que eu escolho entre ?
Você cria um referencial que vai do OBSERVADOR PARA FONTE, se a velocidade estiver no sentido desse referencial, use +, se estiver contrária, use -.
Passo 2
Para o passageiro em repouso, .
Criamos o referencial . Como o som da vuvuzela vai no sentido , então usamos .
Passo 3
Já para o som que vai ser refletido temos que pensar no efeito Doppler de quando ele vai da vuvuzela para a parede, e depois imaginamos a parede como uma fonte sonora (reflexão) e o torcedor como o observador.
Como a parede está em repouso, assim como o passageiro do passo anterior, a frequência que chega até ela é a mesma: .
Na reflexão, a parede vai agir como fonte, , então temos um referencial . O torcedor se afasta da estação, então ele vai no mesmo sentido do referencial, vamos usar :
Resposta
(g) ∼ 250 Hz e ∼ 264Hz.