P1 de Física 2 da USP - 2012

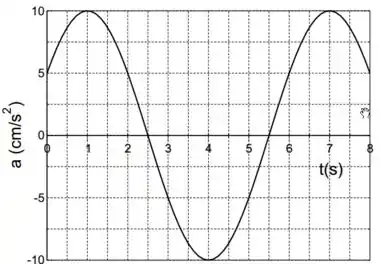
O gráfico abaixo mostra a aceleração em função do tempo de um corpo de massa preso a uma mola ideal de constante em movimento oscilatório. Justificando todas as respostas, determine:

1. O período de oscilação.
2. A amplitude do movimento.
3. A expressão para o deslocamento em função do tempo, em relação ao ponto de equilíbrio.
4. A velocidade do corpo quando
5. A energia mecânica do sistema.

O gráfico ao lado representa a equação horária de um oscilador, para um sistema que é composto por um bloco de massa preso a uma mola de constante elástica que está na posição vertical. Este sistema está imerso em um fluido viscoso com coeficiente de resistência e cuja força de resistência é proporcional à velocidade do corpo que se movimenta em seu interior. Dado que a velocidade inicial do móvel é , responda, sempre considerando o intervalo de tempo mostrado no gráfico:

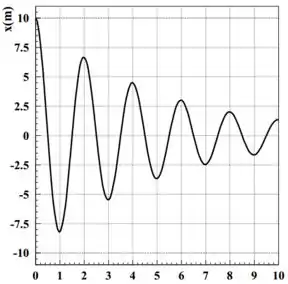
1. Dado o movimento do bloco no sistema descrito acima, qual a equação horária que descreve este sistema? Inclua os valores explícitos de suas constantes.
2. Determine a frequência natural e a constante da mola
3. Qual a velocidade do bloco no instante ?
4. Suponha agora que este mesmo sistema seja retirado do fluido viscoso e passe a oscilar num meio sem resistência. Neste novo regime, o deslocamento máximo é e a constante de fase é nula. Qual será a nova equação horária do sistema?

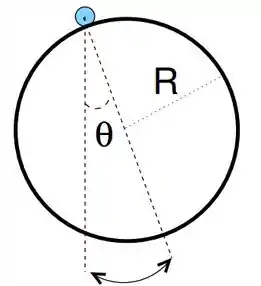
Uma bola de Natal ( esfera oca) de massa e raio é pendurada em um ramo de árvore por um pequeno fio(comprimento desprezível) preso à superfície da esfera(vide figura) e oscila sob a ação da gravidade.

1. Escreva a equação diferencial do movimento para o ângulo que o eixo da bola de Natal faz com a vertical( Vide figura abaixo).
2. Se a bola é deslocada por um ângulo pequeno ( e solto a seguir, calcule a frequência natural de oscilação do sistema.

Considere agora que o atrito do ar gere um torque proporcional à velocidade angular e a área da bola: onde é uma constante ( considere e despreze outros tipos de atrito). Nesse caso:

3. Calcule o fator de qualidade do sistema em termos dos dados do problema.
4. Calcule, em função dos outros dados do problema, o raio máximo da bola para que o regime de amortecimento seja subcrítico.

Dado: Momento de inércia da esfera em relação ao eixo do fio:

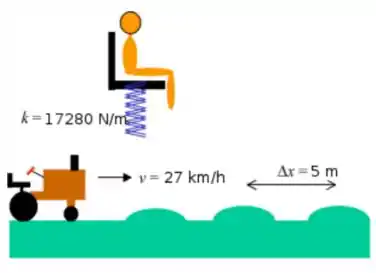
Considere um trator atravessando um campo onde existem ondulações em intervalos regulares. A distância entre cada monte é . Existe uma suspensão de mola ligada ao assento do motorista e este oscila em um regime no qual o amortecimento é desprezível. Podemos assumir uma mola de constante de mola , a massa do assento é e a do motorista é . O trator trafega a . Considere

1. Qual a frequência com que o trator passa em cada elevação?
2. Qual a frequência de oscilação natural do sistema assento-passageiro-mola?
3. Se considerar que, durante o trajeto, a força máxima aplicada pelo trator sobre o sistema cadeira-motorista é de , qual a amplitude máxima do movimento de oscilação do motorista?(assuma que a força é harmônica).
4. Para ocorrer o fenômeno de ressonância entre a força aplicada ao trator pelas ondulações e as oscilações sobre o sistema cadeira-passageiro, qual velocidade o trator deve atingir?(resposta em