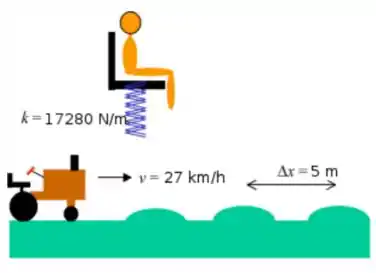
Considere um trator atravessando um campo onde existem ondulações em intervalos regulares. A distância entre cada monte é . Existe uma suspensão de mola ligada ao assento do motorista e este oscila em um regime no qual o amortecimento é desprezível. Podemos assumir uma mola de constante de mola , a massa do assento é e a do motorista é . O trator trafega a . Considere

1. Qual a frequência com que o trator passa em cada elevação?
2. Qual a frequência de oscilação natural do sistema assento-passageiro-mola?
3. Se considerar que, durante o trajeto, a força máxima aplicada pelo trator sobre o sistema cadeira-motorista é de , qual a amplitude máxima do movimento de oscilação do motorista?(assuma que a força é harmônica).
4. Para ocorrer o fenômeno de ressonância entre a força aplicada ao trator pelas ondulações e as oscilações sobre o sistema cadeira-passageiro, qual velocidade o trator deve atingir?(resposta em

b):

A frequência natural pode ser encontrada a partir da frequência angular natural. Essa é dada por:

Só que:

E :

c):

Bom, como você deve ter percebido, a questão se trata de um sistema forçado não amortecido. O sistema natural é a mola com o motorista e a força externa é exercida pelo trator, sendo que essa tem uma frequência

O módulo da amplitude máxima do sistema forçado é:

Calculando

Usando

Logo:

d):

Pra haver ressonância vamos ter que ter: . Como e :

E sabendo que :