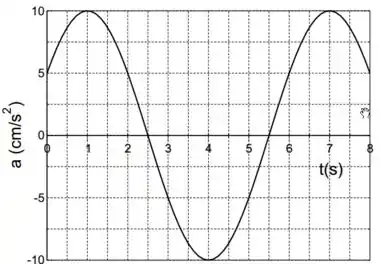
O gráfico abaixo mostra a aceleração em função do tempo de um corpo de massa preso a uma mola ideal de constante em movimento oscilatório. Justificando todas as respostas, determine:
- O período de oscilação.
- A amplitude do movimento.
- A expressão para o deslocamento em função do tempo, em relação ao ponto de equilíbrio.
- A velocidade do corpo quando
- A energia mecânica do sistema.
Passo 1
a):
Pra descobrirmos o período, basta a gente fazer a variação de tempo entre dois picos sucessivos do gráfico da aceleração.
Então:
Passo 2
b):
No MHS a posição é dada por: e a aceleração, a segunda derivada da posição em relação ao tempo, é dada por: .
Bom, a aceleração será máxima quando . Isso é:
Mas pelo gráfico, o módulo da aceleração máxima é . Vamos usar esse valor e o valor de pra calcular .Então;
Logo:
Passo 3
c):
Bom, a função tem uma forma:
Já temos e . Basta acharmos .
Bom, sabemos o valor de quando
Isso é :
ou
Bom, podemos pegar agora outro ponto, como , pra gente descobrir qual dos dois ângulos é o que procuramos.
Logo:
Passo 4
d):
A velocidade será a derivada de
Para
Passo 5
e):
Pro cálculo da energia mecânica do sistema nós podemos usar a teoria que diz:
Mas qual é o valor numérico de Bom, sabemos que é dada por:
Como e :
Então, lembrando que :
Resposta
a):
b):
c):
d):
e):