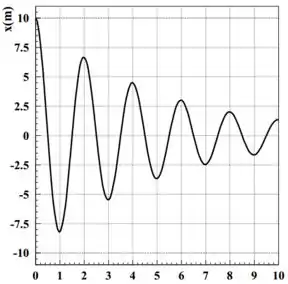
O gráfico ao lado representa a equação horária de um oscilador, para um sistema que é composto por um bloco de massa preso a uma mola de constante elástica que está na posição vertical. Este sistema está imerso em um fluido viscoso com coeficiente de resistência e cuja força de resistência é proporcional à velocidade do corpo que se movimenta em seu interior. Dado que a velocidade inicial do móvel é , responda, sempre considerando o intervalo de tempo mostrado no gráfico:
- Dado o movimento do bloco no sistema descrito acima, qual a equação horária que descreve este sistema? Inclua os valores explícitos de suas constantes.
- Determine a frequência natural e a constante da mola
- Qual a velocidade do bloco no instante ?
- Suponha agora que este mesmo sistema seja retirado do fluido viscoso e passe a oscilar num meio sem resistência. Neste novo regime, o deslocamento máximo é e a constante de fase é nula. Qual será a nova equação horária do sistema?
Passo 1
a):
A equação do MHA tem o formato:
Então vamos procurar cada um dos elementos.
Pelo gráfico, podemos descobrir qual o período da oscilação. Basta a gente pegar os tempos entre dois picos sucessivos. O primeiro pico está em e o segundo em .Logo:
Com isso podemos calcular a frequência angular:
Beleza. Agora vamos calcular o coeficiente de amortecimento . Pela nossa teoria:
Pois, pela amortecida:
Dividindo tudo por :
Então, calculando :
Então : . Logo:
Mas para , então:
Temos outra informação relacionada à velocidade incial. Vamos derivar a equação então:
Pra
Substituindo o valor de :
Usando de novo :
Beleza, agora temos todos os valores pra montar a equação:
As unidades das constantes são:
Passo 2
b):
Bom, a relação entre a frequência do sistema ( e frequência angular natural do mesmo(, é a seguinte:
Isso vem da solução da equação característica da EDO...lembra que temos que resolver essa equação aqui?:
Usando essa aqui:
A gente pode calcular o delta dessa última e as raízes assim:
No fim escrevemos:
É isso ai! Nós chamamos de o . Logo:
E como:
Passo 3
c):
Pra isso a gente vai precisar da derivada da posição. Bom já calculamos isso na a):
Usando os valores de cada constante;
Passo 4
d):
O fator de amortecimento vai se anular, então a equação vai ser uma equação de um MHS, ou seja:
Logo:
Resposta
a):
As unidades das constantes são:
b):
c):
d):