P1 de Física 2 da USP - 2013

Um sistema massa-mola consiste de um corpo de massa e uma mola de constante elástica . No instante de tempo , a massa do sistema é colocada na posição ( em relação à posição de equilíbrio) com velocidade Desprezando quaisquer tipos de atrito, determine:

1. A frequência de oscilação.
2. A amplitude de movimento.
3. A posição em função do tempo
4. A velocidade em função do tempo
5. A energia potencial elástica e a energia cinética em função do tempo.

Um sistema composto por um bloco de massa que se encontra na horizontal, sobre uma mesa, e que está ligada à parede por uma mola, tem seu movimento representado por:

Onde as constantes estão em unidades SI. Despreze o atrito do bloco com a superfície da mesa.

1. Identifique a constante de amortecimento e a frequência angular na equação acima e determine o tipo de amortecimento sofrido pelo sistema.
2. Dado que o bloco se encontra inicialmente na posição , onde a origem deste sistema corresponde à posição do bloco com a mola relaxada, e com velocidade inicial determine a equação horária do sistema em função de sua amplitude e fase inicial.
3. Suponha agora que este sistema passe a oscilar sob a ação de uma força Ache a frequência angular sob qual a amplitude das oscilações é máxima. Assuma que o tempo é grande o suficiente para que a componente transiente do movimento já tenha sido totalmente suprimida. Encontre também esta amplitude máxima.

Um corpo de massa está preso a uma mola de constante elástica O conjunto está colocado ao longo de um eixo em uma região na qual não há aceleração da gravidade, com a outra ponta da mola presa a uma superfície fixa. O corpo está em contato com um martelo e está também sujeita a uma força de resistência do ar dada por:

Para . O sistema é subcrítico, ou seja, temos onde e . Na situação de equilíbrio a superfície do corpo que está em contato com o martelo está na origem do eixo No instante o martelo imprime ao corpo uma velocidade dirigida no sentido positivo do eixo , e depois permanece fixo com a sua superfície de contato em Quando o corpo volta a se chocar com a superfície do martelo, que está em , ele se fixa ao martelo e permanece em repouso após este segundo choque.

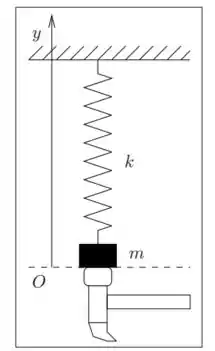
1. Determine a energia mecânica do sistema formado pelo corpo e pela mola em
2. Determine a posição e a velocidade no intervalo de tempo entre os dois choques.
3. Determine o tempo transcorrido entre os dois choques.
4. Determine a energia dissipada no segundo choque do corpo com o martelo.

Uma haste rígida de comprimento e massa está suspensa em um ponto que dista do centro de gravidade da haste. No instante a haste é abandonada a partir do repouso de um ângulo com a direção vertical. Considere o limite de oscilações com ângulos pequenos.

1. Obtenha a equação diferencial que descreve o movimento de rotação da haste.
2. Determine o período de oscilação da haste nessas circunstâncias.
3. Obtenha a solução da equação diferencial.
4. Obtenha a energia mecânica da haste no ângulo .
5. Determine a razão onde é o período de oscilação quando suspensa por sua extremidade.

Formulário adicional: Momento de inércia de uma barra delgada e uniforme de comprimento e massa em relação a um eixo vertical que passa pelo seu centro: