Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Oscilações Forçadas

Ver Teoria
Exercício 211234567891011121314151617181920222324252627282930313233343536

Enunciado

MHA

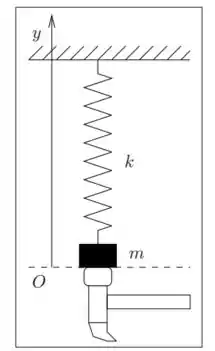
Um corpo de massa m está preso a uma mola de constante elástica k . O conjunto está colocado ao longo de um eixo y em uma região na qual não há aceleração da gravidade, com a outra ponta da mola presa a uma superfície fixa. O corpo está em contato com um martelo e está também sujeita a uma força de resistência do ar dada por:

F a t = - ρ y ˙

Para ρ > 0 . O sistema é subcrítico, ou seja, temos γ < 2 ω 0 , onde γ = ρ m e ω 0 2 = k m . Na situação de equilíbrio a superfície do corpo que está em contato com o martelo está na origem do eixo y . No instante t = 0 o martelo imprime ao corpo uma velocidade v 0 dirigida no sentido positivo do eixo y , e depois permanece fixo com a sua superfície de contato em y = 0 . Quando o corpo volta a se chocar com a superfície do martelo, que está em y = 0 , ele se fixa ao martelo e permanece em repouso após este segundo choque.

  1. Determine a energia mecânica do sistema formado pelo corpo e pela mola em t = 0 .
  2. Determine a posição y ( t ) e a velocidade y ˙ ( t ) no intervalo de tempo entre os dois choques.
  3. Determine o tempo T transcorrido entre os dois choques.
  4. Determine a energia dissipada no segundo choque do corpo com o martelo.

Passo 1

  1. : Em t = 0 não há energia potencial, só energia cinética. Logo:

    2. E M = E c = m v 0 2 2

    Passo 2

  2. : O enunciado nos diz que o regime do problema é subcrítico. Logo, a solução geral do problema é do tipo:

    3. y t = e - γ 2 t ( A c o s ω t + B s e n ( ω t )

    Fazendo t = 0 e usando o valor da posição inicial ( y = 0 ) :

    y 0 = e 0 A c o s 0 + B s e n 0 = 0

    ∴

    A = 0

    Agora vamos analisar a sua derivada, que nos fornece a velocidade (derivando usando a regra do produto):

    y t = e - γ 2 t ( B s e n ω t )

    ∴

    y ˙ t = - γ 2 B e - γ 2 t sin ⁡ ω t + ω B e - γ 2 t c o s ⁡ ( ω t )

    Se liga ai no que fizemos: Reescrevemos aquela expressão que tinha A e B apenas com B , já que A = 0 . Agora vamos substituir o valor de t = 0 ,   lembrando-se que a velocidade inicial é v 0 :

    y ˙ 0 = - γ 2 B e 0 sin ⁡ 0 + ω B e 0 cos ⁡ 0 = v 0

    ∴

    B = v 0 ω

    Show! Com os valores de A e B , basta a gente substituir nas equações acima( y t e y ˙ ( t ) ) :

    y t = e - γ 2 t B s e n ω t   →   y t = v 0 ω e - γ 2 t s e n ω t

    y ˙ t = - γ 2 B e - γ 2 t sin ⁡ ω t + ω B e - γ 2 t cos ⁡ ω t   →   y ˙ t = v 0 e - γ 2 t ( cos ⁡ ω t - γ 2 ω sin ⁡ ω t )

    Passo 3

  3. :

    4. Bom galera, essa aqui é fácil. Vamos olhar a função y t :

    y t = e - γ 2 t ( B s e n ω t )

    Sabemos que o bloquinho sai do y = 0 e volta para o y = 0 . Precisamos descobrir qual o tempo que faz com que isso aconteça. Bom, como a função é uma função com seno, podemos ver que isso vai acontecer quando o seno se igualar a zero:

    s e n ω T = 0   ↔ ω T = π ↔ T = π ω

    Pronto! Só isso (:

    Passo 4

  4. :

Bom, aqui a situação é a seguinte: O nosso bloco atinge o chão com tamanha força que toda a sua energia é dissipada. Como sabemos disso? Por que o enunciado diz que o choque é totalmente inelástico.

Por isso, se a gente descobrir qual é a energia mecânica do sistema logo antes do choque, a gente consegue saber a energia dissipada, pois a energia dissipada será exatamente igual a essa energia mecânica. Show?

Ok, mas quanto vale a energia mecânica logo antes do choque? Bem, como o choque ocorre em y = 0 , não há energia potencial, apenas energia cinética. Bora calcular a velocidade do corpo antes do choque pra depois calcular a energia cinética, então:

y ˙ t = v 0 e - γ 2 t ( cos ⁡ ω t - γ 2 ω sin ⁡ ω t )

O tempo que a o corpo leva pra atingir o martelo foi calculado no item anterior. Logo:

y ˙ π ω = v 0 e - γ 2 π ω ( cos ⁡ π - γ 2 ω sin ⁡ π )

∴

= - v 0 e - γ π 2 ω

Logo, a energia cinética fica:

E c = m 2 - v 0 e - γ π 2 ω 2 = m v 0 2 2 e - γ π 2 ω

Isso é:

E d i s s i p a d a = E c = m v 0 2 2 e - γ π 2 ω

Resposta

  1. : E c = m v 0 2 2
  2. : y t = v 0 ω e - γ 2 t s e n ω t

    3. y ˙ t = v 0 e - γ 2 t ( cos ⁡ ω t - γ 2 ω sin ⁡ ω t )

  3. : T = π ω
  4. : m v 0 2 2 e - γ π 2 ω

Exercícios de Livros Relacionados

54. O bloco de massa m = 45k g é suspenso por duas molas, cada uma com rigidez k = 3k N / m , e está sob a ação da força F = 350 ⋅ cos ⁡ 15 tN onde t é o tempo em segundos. Determine a amplitude X do
Um bloco pesando 20 N oscila na extremidade de uma mola vertica para a qual k = 100 N / m ; a outra extremidade da mola está presa a um teto. Em um certo instante, a mola está esticada 0,30 m além do
13.19E Mostre por substituição direta, que a função x t dada pela Equação 13.73 é solução da Equação 13.61 quando γ = 2 ω 0 .
13.18P Deduza a Equação 13.68.
Desenvolva uma expressão para a transmissibilidade T para o sistema da figura. Essa relação é definida como a força máxima transmitida à base dividida pela amplitude F 0 da função de forçamento. Expre