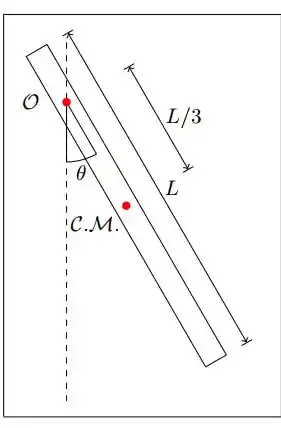
Uma haste rígida de comprimento e massa está suspensa em um ponto que dista do centro de gravidade da haste. No instante a haste é abandonada a partir do repouso de um ângulo com a direção vertical. Considere o limite de oscilações com ângulos pequenos.
- Obtenha a equação diferencial que descreve o movimento de rotação da haste.
- Determine o período de oscilação da haste nessas circunstâncias.
- Obtenha a solução da equação diferencial.
- Obtenha a energia mecânica da haste no ângulo .
- Determine a razão onde é o período de oscilação quando suspensa por sua extremidade.
Formulário adicional: Momento de inércia de uma barra delgada e uniforme de comprimento e massa em relação a um eixo vertical que passa pelo seu centro:
Passo 1
- Pela nossa teoria, sabemos que a equação diferencial de um pêndulo físico fica assim:
- :
- Bom a equação diferencial que estamos tratando é uma EDO. Então a solução geral é do tipo:
- Vamos primeiro dar uma olhada na figura:
- :
Quando .Além disso, temos que calcular o momento de inércia do eixo de rotação, já que esse não passa pelo centro de massa:
Então, a equação fica:
Passo 2
A equação de um MHS pode ser escrita como:
Show! Então podemos identificar na equação de a) a nossa velocidade angular:
Sendo:
Passo 3
O sistema parte do repouso e de um ângulo . Logo:
Substituindo na equação do início:
Passo 4
Pra gente calcular a energia potencial do centro de massa da haste em relação ao nível potencial mais baixo ( Que no nosso caso a gente considerou como a pontinha da haste quando a esticamos), vamos pegar a altura ( Essa continha é tranquila, basta pegar o comprimento total, , e subtrair dele o comprimento devido à inclinação da barra ).
Então a energia mecânica, que é a soma da energia potencial mais a energia cinética, será:
Lembrando que a energia cinética é a energia cinética de rotação. E como , podemos usar a aproximação:
Substituindo na equação de energia mecânica:
Vamos agora usar a expressão de para achar o tempo que o oscilador levou para chegar em :
Pois:
Logo o valor da velocidade quando será ( Vamos antes derivar a função):
Substituindo o valor de , e o valor do momento de inércia na equação da energia mecânica, obteremos:
Com o valor de
Passo 5
Para a haste suspensa pela ponta, fica bem fácil de se calcular a nova equação diferencial. O braço de alavanca do torque do peso agora é , já que o centro de massa da barra está exatamente na metade de seu comprimento. Logo, a equação diferencial será:
Só que quem é esse momento de inércia ai? Bem, é o momento de inércia de um eixo que passa pela ponta da barra. A gente pode calcular ele usando:
Arrumando a equação:
Dividindo todo mundo por :
Mesma história de sempre: :
Logo:
Usando :
Sendo :
Resposta
a):
b):
c):
d):
e):