P2 de Física 2 da USP - 2017

Um bloco de 2 Kg está suspenso por uma mola e oscila verticalmente. Seu movimento é descrito pela equação . Observa-se que a amplitude do movimento se reduz a de seu valor inicial após 2 oscilações. Considerando que estas duas oscilações levam 2 s, determine:

a) O valor numérico dos coeficientes b e c e da constante elástica da mola.

b) Resolva a equação diferencial encontrando y(t) sabendo que o sistema inicia seu movimento na posição de equilíbrio e com velocidade = -12 m/s.

c) Considere agora que este oscilador seja acoplado à uma força externa e passe a oscilar conforme a equação . Encontre a frequência para a qual a amplitude da oscilação seja máxima e a amplitude do movimento para esta frequência. Considere que o tempo durante o qual o sistema está operando é grande o suficiente para que a parte homogênea já tenha decaído.

Considere um bloco de m = 0, 5 kg, preso a uma mola de constante k = 50 N/m. O bloco pode movimentar-se sobre uma superfície horizontal em que um líquido viscoso foi derramado, dando origem a uma força dissipativa proporcional à velocidade, com constante . Uma força externa é aplicada ao bloco, onde e é uma freqüência angular sintonizável.

a) Calcule a potência média transferida pela força externa ao bloco, na situação estacionária, em função de .

b) Encontre a expressão exata da frequência em que essa potência média é máxima. Calcule o valor desta frequência, justificando as aproximações.

c) Suponha agora que a força externa é desligada, qual será a taxa de dissipação de energia do sistema?

O gráfico abaixo representa o valor da amplitude (em metros) em função da razão entre a frequência angular de uma força periódica externa e a frequência angular de um oscilador harmônico. Sabendo-se que esta força atua sobre o oscilador, a partir da observação do gráfico abaixo, podemos afirmar que:

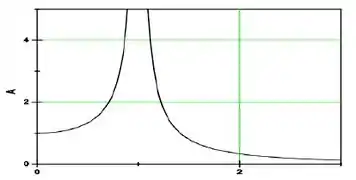
(a) O gráfico representa o comportamento de um sistema oscilatório forçado com amortecimento desprezível. Uma equação diferencial do tipo não é suficiente para analisar este movimento precisamente.

(b) O gráfico representa o comportamento de um sistema oscilatório forçado com amortecimento desprezível. Uma equação diferencial do tipo é suficiente para analisar este movimento precisamente.

(c) O gráfico representa o comportamento de um sistema oscilatório forçado com fator de amortecimento não desprezível, mas menor que . Uma equação diferencial do tipo é suficiente para analisar este movimento precisamente.

(d) O gráfico representa o comportamento de um sistema oscilatório forçado com fator de amortecimento não desprezível, mas menor que . Uma equação diferencial do tipo não é suficiente para analisar este movimento precisamente.

(e) O gráfico representa o comportamento de um sistema oscilatório forçado com fator de amortecimento forte e maior do que . Uma equação diferencial do tipo é suficiente para analisar este movimento precisamente.

Um circuito elétrico constituído por um resistor R, um capacitor C e um indutor L, está ligado e possui corrente elétrica I. Sabendo que a equação diferencial que representa este sistema é dada por onde V(t) é a diferença de potencial aplicada ao circuito e que varia com o tempo. Determine qual afirmativa abaixo é correta:

(a) Esta equação corresponde à de um oscilador harmônico forçado, cuja frequência angular da solução homogênea é dada por .

(b) Esta equação corresponde à de um oscilador harmônico amortecido, cuja frequência angular da solução homogênea é dada por .

(c) Esta equação corresponde à de um oscilador harmônico forçado, cuja frequência angular da equação homogênea é dada por .

(d) Esta equação não corresponde à de um oscilador harmônico dado que o resistor, capacitor e indutor não oscilam.

(e) Esta equação não corresponde à de um oscilador harmônico dado que a diferença de potencial não oscila.

Um sistema massa-mola é imerso num meio viscoso, com constante de amortecimento e constante de mola . Uma força externa de frequência angular atua sobre a massa. Qual deve ser o valor da massa para que a amplitude do movimento seja máxima?

(a) 4 kg

(b) 35 g

(c) 40 g

(d) 350 g

(e) 35 kg

Uma partícula de massa m obedece à lei horária para a posição conforme a figura, onde x é dado em metros e t em segundos.

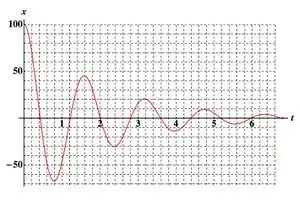
Indique a afirmação abaixo que é compatível com a figura:

(a) O sistema corresponde a amortecimento subcrítico, com e .

(b) O sistema corresponde a amortecimento supercrítico, com e .

(c) O sistema corresponde a amortecimento subcrítico, com e .

(d) O sistema corresponde a amortecimento crítico, com .

(e) O sistema corresponde a amortecimento supercrítico, com e .