O gráfico abaixo representa o valor da amplitude (em metros) em função da razão entre a frequência angular de uma força periódica externa e a frequência angular de um oscilador harmônico. Sabendo-se que esta força atua sobre o oscilador, a partir da observação do gráfico abaixo, podemos afirmar que:
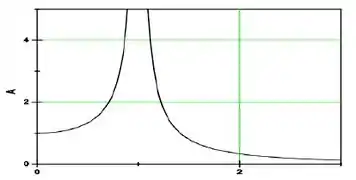
(a) O gráfico representa o comportamento de um sistema oscilatório forçado com amortecimento desprezível. Uma equação diferencial do tipo não é suficiente para analisar este movimento precisamente.
(b) O gráfico representa o comportamento de um sistema oscilatório forçado com amortecimento desprezível. Uma equação diferencial do tipo é suficiente para analisar este movimento precisamente.
(c) O gráfico representa o comportamento de um sistema oscilatório forçado com fator de amortecimento não desprezível, mas menor que . Uma equação diferencial do tipo é suficiente para analisar este movimento precisamente.
(d) O gráfico representa o comportamento de um sistema oscilatório forçado com fator de amortecimento não desprezível, mas menor que . Uma equação diferencial do tipo não é suficiente para analisar este movimento precisamente.
(e) O gráfico representa o comportamento de um sistema oscilatório forçado com fator de amortecimento forte e maior do que . Uma equação diferencial do tipo é suficiente para analisar este movimento precisamente.
Passo 1
Pelo gráfico podemos ver que a amplitude vai pra infinito quando a razão entre as frequências é 1. Ou seja, quando:
E essa questão tem uma pegadinha! Porque a gente sabe que em oscilações forçadas amortecidas, na ressonância, a amplitude atinge um máximo, mas não vai pro infinito. Isso acontece em oscilações forçadas sem amortecimento.
A amplitude máxima no MHA forçado acontece quando a frequência da força externa é:
Como na amplitude máxima:
Ou seja, o amortecimento é desprezível.
Nisso a gente já mata todas as alternativas que dizem que o amortecimento não é desprezível (c, d e e).
Agora temos que pensar: a equação do MHA forçado é suficiente pra descrever o movimento?
Não! No MHA forçado, na ressonância, a amplitude atinge um valor máximo, mas não vai pro infinito. Diferente do que tá acontecendo nessa questão, em que as amplitudes tão muito grandes!
Em amplitudes grandes assim, não podemos garantir que vai ter linearidade entre o amortecimento e a força externa. Então não podemos usar a equação do MHA forçado pra descrever o movimento.
A resposta então vai ser a alternativa A.
Resposta
Letra A.