Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento Harmônico Amortecido

Ver Teoria
Exercício 2012345678910111213141516171819212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768

Enunciado

Uma partícula de massa m obedece à lei horária para a posição conforme a figura, onde x é dado em metros e t em segundos.

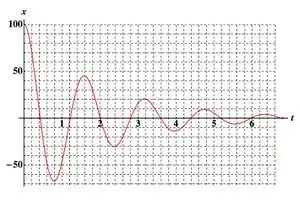
Indique a afirmação abaixo que é compatível com a figura:

(a) O sistema corresponde a amortecimento subcrítico, com γ ≈ 0,9   s - 1 e ω ≈   4   s - 1 .

(b) O sistema corresponde a amortecimento supercrítico, com γ ≈ 1,6   s - 1 e β ≈   0,8   s - 1 .

(c) O sistema corresponde a amortecimento subcrítico, com γ ≈ 1,6   s - 1 e ω ≈   2   s - 1 .

(d) O sistema corresponde a amortecimento crítico, com γ ≈ 0,9   s - 1 .

(e) O sistema corresponde a amortecimento supercrítico, com γ ≈ 0,9   s - 1 e β ≈   4   s - 1 .

Passo 1

O sistema corresponde ao amortecimento subcrítico! Que é o único que oscila. Isso nós devemos saber olhando pro gráfico, atenção!

O período vai ser:

T = 1,6   s

Isso também olhando no gráfico, porque é o tempo entre duas cristas ou dois vales.

E a frequência angular conseguimos achar:

ω = 2 π T = 2 π 1,6

ω ≅ 3,92 ≅ 4   r a d / s

Show! Agora precisamos achar γ .

O regime de amortecimento subcrítico tem amplitude:

A t = A e - γ t / 2

Vou tirar dois dados do gráfico:

A 0 = A = 100

A 3,2 = A e - 1,6 γ = 20

Então:

e - 1,6 γ = 20 100 = 1 / 5

- 1,6 γ = ln ⁡ 1 / 5

γ ≅ 0,9   s - 1

Resposta

Letra A.

Exercícios de Livros Relacionados

137. Uma máquina de 200k g se apoia sobre quatro suportes no chão, cada um dos quais possui uma constante de mola efetiva k = 250k N / m e um coeficiente de amortecimento viscoso efetivo c = 1000 N ⋅
138. Represente graficamente a resposta x do corpo de 20k g ao longo do intervalo de tempo 0 ≤ t ≤ 1 segundo. Determine os valores máximo e mínimo de x e seus respectivos instantes de tempo. As condiç
Para uma criança em um balanço, a amplitude cai em um fator de 1 e em cerca de oito períodos, se nenhuma energia mecânica adicional for fornecida ao sistema. Estime o fator Q para este sistema.
Para o cilindro do Prob. 8/8, determine o deslocamento vertical x, medido para baixo no sentido positivo em milímetros, a partir da posição de equilibro, em termos do tempo t, em segundos, medido a pa
Em um oscilador amortecido com m = 250 g , k = 85 N / m e b = 70 g / s , qual é a razão entre a amplitude das oscilações amortecidas e a amplitude inicial após 20 ciclos?