PSUB de Física 2 da USP - 2017

Se as funções de ondas de pressão, densidade e deslocamento de uma onda sonora harmônica progressiva são, respectivamente p(x, t), ρ (x, t) e u(x, t) podemos dizer que:

(a) u(x, t) e p(x, t) estão em quadratura.

(b) u(x, t) e p(x, t) estão em fase.

(c) p(x, t) e ρ (x, t) estão em quadratura.

(d) A diferença de fase entre p(x, t) e ρ(x, t) é de π.

(e) As três funções estão sempre em fase.

Qual das seguintes alternativas é certa para a função:

Onde x e y estão dados em metros quando t é expressado em segundos?

(a) y(x, t) representa uma onda progressiva que em 6 s percorre uma distancia de 8 m.

(b) y(x, t) representa uma onda progressiva com uma velocidade de propagação de 4 m/s.

(c) y(x, t) representa uma onda progressiva que se movimenta no sentido positivo do eixo x.

(d) y(x, t) não representa uma onda progressiva.

(e) y(x, t) representa uma onda progressiva tranversal onde o máximo deslocamento vertical é 0,5 m.

Dada uma massa m apoiada sobre um pistão pneumático com um amortecimento r, queremos ajustar a constante de mola k atuando sobre o sistema de forma que, diante de uma perturbação externa, ele tenha um retorno no menor tempo possível.

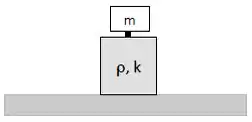
A equação de movimento do corpo na ausência de forças externas é dada por:

a) Qual o valor de k que faz o sistema voltar ao equillíbrio no menor tempo possível? Neste caso, qual a forma geral da solução da equação diferencial acima? Justifique sua resposta.

b) Se em t = 0 o corpo, inicialmente em equilíbrio, recebe uma pancada, transferindo um impulso vertical p, qual a função y(t) que representa a evolução da posição do corpo?

c) Se uma vibração externa é aplicada com frequência Ω, e uma força , qual a expressão da amplitude de oscilação A(Ω)? Para que valor de Ω a amplitude de oscilação é máxima?

Um pêndulo de torção de massa M = 5, 0 kg, imerso em um meio viscoso, oscila em torno do seu ponto de equilíbrio obedecendo a seguinte equação de movimento:

Onde: , e

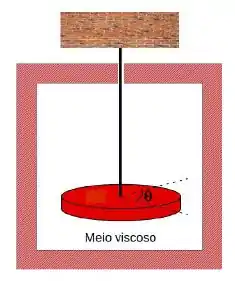
A equação de movimento que satisfaz as condições iniciais:

É dada por:

(a)

(b)

(c)

(d)

(e)

Um tubo aberto pelas duas extremidades pode gerar ondas estacionárias de freqüências e , mas nenhuma onda estacionária pode ser gerada para freqüências entre essas duas. Pode-se dizer que:

(a) não correspondem, respetivamente, com as freqüências de vibração do primeiro e segundo harmônicos da onda estacionária.

(b) correspondem, respetivamente, as freqüências de vibração do primeiro e segundo harmônicos da onda estacionária.

(c) corresponde à freqüência do primeiro harmônico da onda estacionária, mas não é a freqüência do segundo harmônico.

(d) não é a freqüência de vibração do primeiro harmônico da onda estacionária, e corresponde à frequência associada ao segundo harmônico.

(e) correspondem, respetivamente, as freqüências do segundo e terceiro harmônicos da onda estacionária.

Um carro com velocidade = 120 km/h aproxima-se de outro, com velocidade = 100 km/h, ambos dirigindo para o mesmo sentido. Os motoristas buzinam um para o outro, e uma pessoa na estrada, entre os dois carros, ouve um tom com um batimento. Sendo as frequências das buzinas dos carros e , respectivamente determine:

a) Qual a expressão para a frequência do batimento, em função das frequências e ?

b) Qual a expressão para a frequência percebida pela pessoa, em função das frequências e ?

c) Se a pessoa percebe um tom a 215 Hz, com um batimento de período T = 0, 1s, quais os valores de e ?