Um carro com velocidade = 120 km/h aproxima-se de outro, com velocidade = 100 km/h, ambos dirigindo para o mesmo sentido. Os motoristas buzinam um para o outro, e uma pessoa na estrada, entre os dois carros, ouve um tom com um batimento. Sendo as frequências das buzinas dos carros e , respectivamente determine:

a) Qual a expressão para a frequência do batimento, em função das frequências e ?
b) Qual a expressão para a frequência percebida pela pessoa, em função das frequências e ?
c) Se a pessoa percebe um tom a 215 Hz, com um batimento de período T = 0, 1s, quais os valores de e ?
Passo 1
a) Eita, essa questão tá misturando Efeito Dopler com Batimento.

Mas calma, tá tudo sob controle. (Eu acho.)

Então! Primeiro vamos calcular as frequências percebidas pelo observador. A gente usa essa fórmula:
Em que os subscritos o e f correspondem a observador e fonte. Os sinas a gente faz assim: referencial sempre positivo do observador pra fonte.
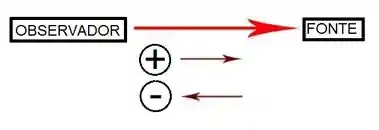
Para o carro 1:
Como ele mandou considerar a velocidade do som igual a 1200 km/h:
Para o carro 2:
E a frequência de batimento vai ser:
Passo 2
b) A frequência percebida vai ser a média das duas frequências. Ou seja:
Passo 3
c) Então, ele deu duas informações pra gente.
Primeiro que a frequência percebida é de 215 Hz. Ou seja, a frequência MÉDIA é de 215 Hz.
A outra informação foi que a frequência de batimento é de:
Passo 4
Para a frequência de batimento nós temos duas hipóteses:
E então:
Com isso:
E então:
Com isso:
Resposta
a)
b)
c) e ou e