P2 de Física 3 - FIS1051 da PUCRIO - 2020.1

Uma partícula pontual de massa m e carga (positiva) se move com velocidade de módulo constante de tal forma que, como mostra a Figura 1, sua trajetória é descrita pela linha tracejada. Essa partícula penetra em uma região de campo magnético constante (região cinza- escuro) e realiza um movimento circular de raio (ao longo de um arco de graus). Em seguida, penetra em outra região de campo magnético constante (região cinza-claro) e realiza um movimento circular de raio r (ao longo de um arco de graus). Observe que :

1. Calcule a razão (módulos dos campos magnéticos).
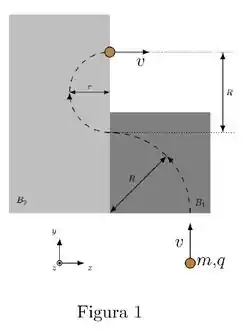
2. m = 1,0 × 10 - 3 k g , , e , encontre os vetores campos magnéticos em ambas as regiões.

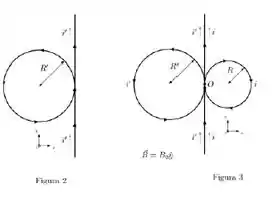
Uma corrente i percorre um fio muito longo. O fio está posicionado inicialmente de maneira vertical. Em certo ponto, realiza um loop circular de raio e retorna à mesma orientação vertical, como mostra a Figura 1. Embora extremamente próximos, não há contato entre os pontos inicial e final do loop.

Com relação ao ponto C marcado na figura, calcule, utilizando a lei de Biot-Savart explicitamente:

1. O vetor campo magnético devido ao loop.
2. o vetor campo magnético devido a cada uma das duas seções retas do fio

Considere agora outra configuração, onde uma nova corrente i’ percorre um segundo fio também muito longo. Mais uma vez, o fio está posicionado inicialmente de maneira vertical e, em certo ponto, realiza um loop circular de raio , retornado à mesma orientação vertical, como mostra a Figura 2. Embora extremamente próximos, não há contato entre os pontos inicial e final do loop.

Em seguida, esse fio é colocado bem próximo (mais uma vez, sem contato) ao primeiro fio, como mostra a Figura 3. No sistema descrito pela Figura 3, existe um campo magnético constante .

3. Qual deve ser a relação entre as correntes e para que o torque resultante devido ao campo magnético sobre o conjunto de loops seja nulo?

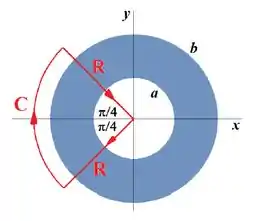
Um fio reto, infinito e oco (de raio interno e externo ) centrado no eixo tem a seção transversal (no plano mostrada na Figura. Este fio é percorrido por corrente com densidadeno sentido , onde . Determine:

1. A corrente total em seção transversal arbitrária do fio.
2. O vetor do campo magnético em um ponto arbitrário cuja distância ao eixo é
3. O vetor do campo magnético em um ponto arbitrário cuja distância ao eixo é
4. O vetor do campo magnético em um ponto arbitrário cuja distância ao eixo é
5. O valor de ao longo do contorno orientado mostrado na figura, formado por duas radiais de comprimento e um quadrante de círculo de mesmo raio.

Em uma região de campo magnético uniforme , um aro condutor circular de raio está localizado no plano . Suponha que a resistência deste aro seja constante e igual a . Suponha que:

Onde é uma constante de tempo desconhecida.

1. Desenhe um esquema mostrando o aro, a direção do campo magnético, a direção da corrente induzida no aro e a força sobre o aro devida ao campo magnético.
2. Calcule o fluxo magnético e a sobre o aro. Obtenha expressões para a corrente induzida e para o valor da força magnética agindo sobre um segundo do aro de comprimento .
3. Calcule a potencia instantânea dissipada no aro por efeito Joule.
4. Suponha que forças externas agindo uniformemente sobre o aro, na direção radial, são responsáveis pelo aumento do raio do aro. Calcule a potência em um certo instante de tempo que as forças externas realizam sobre o aro. Despreze qualquer energia elástica do material que constitui o aro. É possível dizer que ? Justifique sua afirmação.

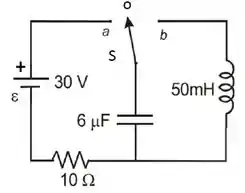
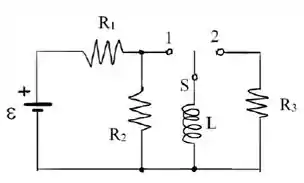
No circuito da figura ao lado, o capacitor está inicialmente descarregado e a corrente no indutor é nula. A chave está inicialmente na posição central ().

A chave passa então para a posição , onde permanece durante um tempo equivalente a duas constantes de tempo capacitivas. Em seguida (no novo instante de tempo ), passa para a posição , na qual permanece por um tempo muito longo.

1. Determine a expressão da corrente que percorre o indutor em função do tempo. Qual é o valor da amplitude máxima da corrente?
2. Trace os gráficos das variações da corrente no indutor e da carga no capacitor em função do tempo quando a chave está na posição .
3. Determine a energia total armazenada no circuito .

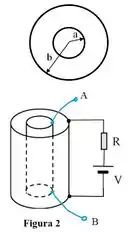
Dois solenoides cilíndricos, de raios e comprimento são colocados um dentro do outro, como mostra a figura ao lado. O solenoide de raio tem espiras por unidade de comprimento e o solenoide de raio possui espiras por unidade de comprimento.

No instante , os terminais do solenoide de raio (o maior) são ligados a uma bateria de . V e um resistor, como mostra a Figura 2.

1. Escreva a expressão para a corrente no solenoide de raio em função do tempo.
2. Escreva a expressão para o fluxo magnético total no solenoide de raio em função do tempo.
3. Escreva a expressão para o módulo da entre os terminais d solenoide de raio , mostrados como e na figura em função do tempo.
4. Suponha que forças externas agindo uniformemente sobre o aro, na direção radial, são responsáveis pelo aumento do raio do aro. Calcule a potência em um certo instante de tempo que as forças externas realizam sobre o aro. Despreze qualquer energia elástica do material que constitui o aro. É possível dizer que ? Justifique sua afirmação.

No circuito da figura abaixo, tem-se e as seguintes fases sucessivas:

− Fase 1: chave na posição durante longo tempo;

− Fase 2: chave na posição durante longo tempo.

1. Determine o valor de para que a tensão no indutor no inicio da fase seja igual a .
2. Calcule o valor e o sentido das correntes que passam pelo resistor e no indutor no inicio e no fim da fase .
3. Determine a expressão da corrente em na fase . Qual é o sentido da corrente em ?
4. Calcule a energia dissipada em na fase .

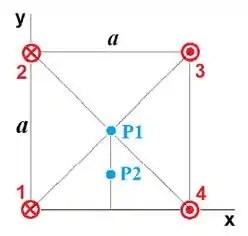
Os quatro fios retos, infinitos e paralelos ao eixo estão dispostos nos vértices de um quadrado de lado e têm correntes de mesmo módulo. Os sentidos das correntes e as posições dos fios estão indicados na Figura. Determinar o vetor campo magnético total (devido a todos os fios) nos pontos:

1. de coordenadas .
2. de coordenadas .
3. 1,2 e sobre o fio .