PUC-RIO – Física 3 2020.1 – P2– Questão 7
No circuito da figura abaixo, tem-se e as seguintes fases sucessivas:
− Fase 1: chave na posição durante longo tempo;
− Fase 2: chave na posição durante longo tempo.
- Determine o valor de para que a tensão no indutor no inicio da fase seja igual a .
- Calcule o valor e o sentido das correntes que passam pelo resistor e no indutor no inicio e no fim da fase .
- Determine a expressão da corrente em na fase . Qual é o sentido da corrente em ?
- Calcule a energia dissipada em na fase .
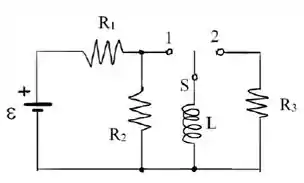
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
No final da fase o fio que tem o indutor se comporta como um fio em curto, e daí o circuito resultante é simples e composto pela bateria e pela resistência :
E esta corrente é a mesma que continua circulando no inicio da fase , que é composto pelo indutor e pelo resistor . Então a no indutor é a mesma ddp em :
Passo 2
Letra (b):
No início da fase o se comporta como um circuito aberto, então temos um circuito composto pela bateria e duas resistências em série:
O sentido dessa corrente é para baixo e no não circula corrente.
No fim da fase as coisas se invertem, temos que no indutor a corrente é máxima e em não há :
E em agora não há corrente circulando.
Tranquilo? Vamos para o último item?
Passo 3
Letra (c):
Durante a fase a expressão da corrente em é:
E a constante é:
A corrente é , e assim podemos achar :
O sentido da corrente que circula em é para cima já que a corrente circula para baixo em , conservando o sentido que tinha no final da fase .
Tranquilo? Vamos para o último item?
Passo 4
Letra (d):
A energia dissipada em coincide com a energia armazenada no indutor :
Beleza?
Pronto pra próxima questão? =)