Em uma região de campo magnético uniforme , um aro condutor circular de raio está localizado no plano . Suponha que a resistência deste aro seja constante e igual a . Suponha que:
Onde é uma constante de tempo desconhecida.
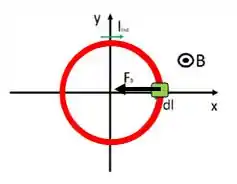
- Desenhe um esquema mostrando o aro, a direção do campo magnético, a direção da corrente induzida no aro e a força sobre o aro devida ao campo magnético.
- Calcule o fluxo magnético e a sobre o aro. Obtenha expressões para a corrente induzida e para o valor da força magnética agindo sobre um segundo do aro de comprimento .
- Calcule a potencia instantânea dissipada no aro por efeito Joule.
- Suponha que forças externas agindo uniformemente sobre o aro, na direção radial, são responsáveis pelo aumento do raio do aro. Calcule a potência em um certo instante de tempo que as forças externas realizam sobre o aro. Despreze qualquer energia elástica do material que constitui o aro. É possível dizer que ? Justifique sua afirmação.
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
Passo 2
Letra (b):
O fluxo magnético é o produto da área pelo campo. A expressão do campo foi dada e a área é a área da espira de raio , então o fluxo é:
A fem induzida é dada pela derivada temporal do fluxo, então vamos à derivada:
E a corrente induzida é dada pela lei de ohm “quem vê U RI”:
E a força magnética é radial para dentro agindo sobre o elemento de aro é:
Tranquilo?
Passo 3
Letra (c):
Agora queremos saber a potencia dissipada por efeito joule. Com uma resistência e corrente a potencia dissipada é:
Agora é só substituir:
Vamos para o último item?
Passo 4
Letra (d):
A força externa aumenta o aro a uma taxa de:
Assim, a potencia externa realizada pela força externa, que se opõe á força magnética apenas (o aro não gira, é sempre bom lembrar!) é positiva (ambas, força externa e velocidade do elemento do aro ao radiais para fora):
E somando sobre todos os elementos temos que , daí a potência externa fica:
A razão para a potencia externa ser maior que a potencia dissipada é que alem de injetar a energia perdida na resistência , a potência injetada tem que alimentar de energia um indutor cada vez maior, o aro! Olha que louco!
Beleza?
Pronto pra próxima questão? =)
Resposta
A razão para a potência externa ser maior que a potência dissipada é que alem de injetar a energia perdida na resistência , a potência injetada tem que alimentar de energia um indutor cada vez maior, o aro!