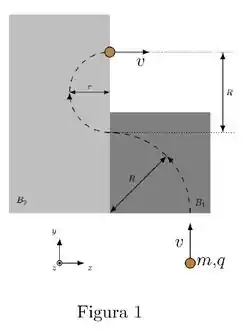
Uma partícula pontual de massa m e carga (positiva) se move com velocidade de módulo constante de tal forma que, como mostra a Figura 1, sua trajetória é descrita pela linha tracejada. Essa partícula penetra em uma região de campo magnético constante (região cinza- escuro) e realiza um movimento circular de raio (ao longo de um arco de graus). Em seguida, penetra em outra região de campo magnético constante (região cinza-claro) e realiza um movimento circular de raio r (ao longo de um arco de graus). Observe que :

1. Calcule a razão (módulos dos campos magnéticos).
2. m = 1,0 × 10 - 3 k g , , e , encontre os vetores campos magnéticos em ambas as regiões.

Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?

Letra (a):

Temos uma partícula pontual, certo? (aqui não é o caso de uma distribuição de cargas, por exemplo) então a velocidade será constante em módulo, certo?

Como temos um movimento circular constante, a força centrípeta precisa ser igual a força magnética em ambos os casos! Então a ideia aqui é relembrar como se calculam essas duas forças, fazer a igualdade da velocidade e assim chegar na relação dos campos, beleza?

A força centrípeta é:

E a força magnética é:

Agora vamos aplicar isso às regiões.

Vamos ver na primeira região, com campo :

A igualdade que queremos é:

Então agora é só substituir o raio e o campo :

Assim a expressão para a velocidade é:

Certo? agora vou fazer isso pra região de campo e raio :

Então agora é só substituir o raio e o campo :

Assim a expressão para a velocidade é:

E por fim, sabemos que essas velocidades são iguais em módulo, então podemos igualar essas duas expressões, saca só:

A massa e a carga da partícula são as mesmas, então manipulando um pouquinho essa expressão ficamos com a relação da razão dos campos:

E ainda podemos simplificar ainda mais, pois lá do finalzinho do enunciado, ele nos diz que :

Tai a relação entre os campos: .