PUC-RIO – Física 3 2020.1 – P2– Questão 6
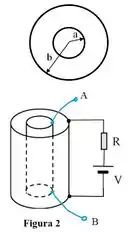
Dois solenoides cilíndricos, de raios e comprimento são colocados um dentro do outro, como mostra a figura ao lado. O solenoide de raio tem espiras por unidade de comprimento e o solenoide de raio possui espiras por unidade de comprimento.
No instante , os terminais do solenoide de raio (o maior) são ligados a uma bateria de . V e um resistor, como mostra a Figura 2.
- Escreva a expressão para a corrente no solenoide de raio em função do tempo.
- Escreva a expressão para o fluxo magnético total no solenoide de raio em função do tempo.
- Escreva a expressão para o módulo da entre os terminais d solenoide de raio , mostrados como e na figura em função do tempo.
- Suponha que forças externas agindo uniformemente sobre o aro, na direção radial, são responsáveis pelo aumento do raio do aro. Calcule a potência em um certo instante de tempo que as forças externas realizam sobre o aro. Despreze qualquer energia elástica do material que constitui o aro. É possível dizer que ? Justifique sua afirmação.
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
A indutância desse solenoide é , então a corrente obedece a seguinte equação diferencial:
No instante temos , então agora é resolver essa equação:
E integrando dos dois lados temos:
E isolando a corrente temos:
E agora para encontrar o valor de fazemos assim:
E a corrente por fim é:
Passo 2
Letra (b):
O fluxo magnético no solenoide interno é:
Tranquilo? Vamos para o último item?
Passo 3
Letra (c):
E a ddp no solenoide de raio pode ser encontrada por meio da derivada temporal do fluxo que a gente acabou de encontrar:
Beleza?
Pronto pra próxima questão? =)